
| A. | “x<0”是“ln(x+1)<0”的充要条件 | |
| B. | “?x≥2,x2-3x+2≥0”的否定是“?x<2,x2-3x+2<0” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,17,29,41,53的同学均被选出,则该班学生人数可能为65 | |
| D. | 在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则随机变量X的期望$E(X)=\frac{Mn}{N}$ |
分析 对4个选项,分别进行判断,即可得出结论.
解答 解:对于A,由ln(x+1)<0,得:0<x+1<1,解得:-1<x<0,故x<0是-1<x<0的必要不充分条件,不正确;
对于B,“?x≥2,x2-3x+2≥0”的否定是“?x≥2,x2-3x+2<0”,不正确;
对于C,学号为5,17,29,41,53的同学,样本间隔为17-5=12,则人数为12×5=60,应该是60人,故不正确;
对于D,含有M件次品的N件产品中,任取n件,其中恰有X件次品,则随机变量X的期望$E(X)=\frac{Mn}{N}$,正确.
故选:D.
点评 本题考查命题的真假判断,考查充要条件的判定,命题的否定,系统抽样,期望,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
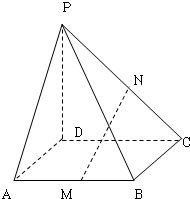 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N分别是AB,PC的中点;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com