Question

10．一艘海监船在某海域实施巡航监视，由A岛向正北方向行驶80海里至M处，然后沿东偏南30°方向行驶50海里至N处，再沿南偏东30°方向行驶30$\sqrt{3}$海里至B岛，则A，B两岛之间距离是70海里．

Answer 1

分析 首先作出辅助线连接AN构造出三角形，然后在△AMN中连续两次运用余弦定理可得出AN和cos∠MAN的值，再由cos∠ANB=cos（30°+∠MAN）即可得出其余弦值，最后在△ANB中运用余弦定理即可得出所求的结果．

解答 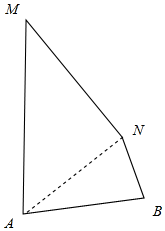解：连接AN，则在△AMN中，应用余弦定理可得AN=$\sqrt{8{0}^{2}+5{0}^{2}-2×80×50×\frac{1}{2}}$=70，
∴cos∠MAN=$\frac{6400+4900-2500}{2×80×70}$=$\frac{11}{14}$
∴cos∠ANB=cos（30°+∠MAN）=$\frac{3\sqrt{3}}{14}$
∴AB=$\sqrt{4900+2700-2×70×30\sqrt{3}×\frac{3\sqrt{3}}{14}}$=70，
故答案为70．

点评 本题主要考查了余弦定理在解三角形中的应用、两角差的余弦公式和同角三角函数的基本关系，属中档题．