Question

9．点P是双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$上的点，F₁，F₂分别是双曲线的左右焦点，$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，则|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=（　　）

• A． 48
• B． 32
• C． 16
• D． 24

Answer 1

分析 根据双曲线的方程得到a，c的值，设|$\overrightarrow{P{F}_{1}}$|=m，|$\overrightarrow{P{F}_{2}}$|=n，根据双曲线的定义可得n-m=4，再根据垂直和勾股定理可得答案

解答 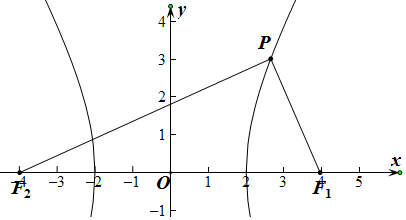解：设|$\overrightarrow{P{F}_{1}}$|=m，|$\overrightarrow{P{F}_{2}}$|=n，
∵a=2，c=4，
∴n-m=2a=4，
∴（n-m）²=16，
即n²+m²-2mn=16
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，
∴$\overrightarrow{P{F}_{1}}$⊥$\overrightarrow{P{F}_{2}}$，
∴n²+m²=4c²=64，
∴64-2mn=16，
∴mn=24，
即|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=24，
故选：D

点评 本题考查了双曲线的简单性质，以及向量的数量积和向量的垂直的关系，属于基础题．