Question

 

已知关于x的方程|x²+ax+b|=2，（其中a、b∈R）的解集为M，且M中有三个元素.

   （1）求b=f(a)的表达式.

   （2）请求出M中元素恰好为直角三角形三边长的充要条件.

 

 

 

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 （1）原方程等价于x²+ax+b=2和x²+ax+b－2，

    其中判别式分别为△₁=ab+8，△₂=ab－8，……………………2分

    ∵△₁>△₂，而M中有三个元素，

∴△₂=0，即ab－8=0

…………………………………………………………6分

   （2）由（1）知，ab=8，

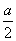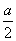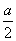∴由求根公式解出原方程的解为－，－－2，－+2.

①必要性，由于以这三个元素恰好为直角三角形三边长，

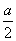∴（－）²+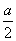（－－2）²=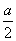（－+2）²，解得a=－16，从而b=62.…………8分

②充分性。如果a=－16,b=62，则可得方程的解集为M={10，6，8}.

这时三个元素恰为直角三角形的三边长.

∴所求的充要条件是a－16,b=62.…………………………………………12分