
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
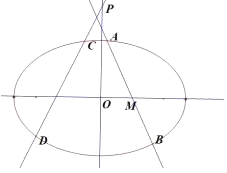
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() (点
(点![]() 在点
在点![]() 的上方),试求
的上方),试求![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() ),使得
),使得![]() 到直线
到直线![]() 的距离
的距离![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)1;(3)存在,4.
;(2)1;(3)存在,4.
【解析】
(1)根据椭圆的焦距求出c,由P(0,2)关于直线y=﹣x的对称点在椭圆Γ上可得a=2,即可求出b2,可得椭圆方程;
(2)设过点P(0,2)的直线方程为y=mx+2,代入椭圆方程,运用韦达定理,弦长公式和点到直线的距离,表示出三角形的面积,再根据函数的性质即可求出最值;
(3)设直线l的方程为y=k(x﹣1),代入椭圆方程,运用韦达定理,假设存在这样的直线l0,运用点到直线的距离公式和两点的距离公式,可得![]() ,化简整理代入,即可判断.
,化简整理代入,即可判断.
(1)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
因为![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,又
,又![]() ,故
,故![]() ,
,
则![]() .所以,椭圆
.所以,椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意,直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() ,
,
由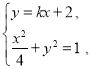 得
得![]() ,
,
由△![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,
所以,![]()
![]() .
.
令![]() ,则
,则![]() ,所以,
,所以,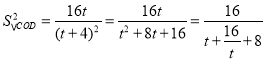 ,
,
因为![]() (当且仅当
(当且仅当![]() 时等号成立),此时
时等号成立),此时![]() .
.
所以,当且仅当![]() ,即
,即![]() 时,△
时,△![]() 的面积取最大值
的面积取最大值![]() .
.
(3)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程为
的方程为![]() ,此时
,此时![]() ,
,![]() ,
,
等式![]() 成立;
成立;
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由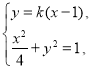 得
得![]() ,
,
span>设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
由题意,![]() 与
与![]() 一个小于
一个小于![]() ,另一个大于
,另一个大于![]() ,不妨设
,不妨设![]() ,
,
则![]()
![]()
![]()
![]()
![]() ,
,
所以,![]() ,
,
即![]() ,解得
,解得![]() .
.
综上,存在满足条件的直线![]() ,使得
,使得![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.命题“p且q”为真,则![]() 恰有一个为真命题
恰有一个为真命题
B.命题“已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件”
”的充分不必要条件”
C.命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]()
D.如果函数![]() 在区间
在区间![]() 上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有![]() ,那么函数
,那么函数![]() 在区间
在区间![]() 内有零点
内有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个半径为12厘米圆心角为![]() 的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
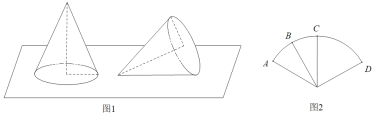
(1)无底圆锥被一阵风吹倒后(如图1),求它的最高点到水平面的距离;
(2)扇形纸片PAD上(如图2),C是弧AD的中点,B是弧AC的中点,卷成无底圆锥后,求异面直线PA与BC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车是我国汽车工业由大变强的一条必经之路!国家对其给予政策上的扶持,己成为我国的战略方针.近年来,我国新能源汽车制造蓬勃发展,某著名车企自主创新,研发了一款新能源汽车,经过大数据分析获得:在某种路面上,该品牌汽车的刹车距离![]() (米)与其车速
(米)与其车速![]() (千米/小时)满足下列关系:
(千米/小时)满足下列关系:![]() (
(![]() ,
,![]() 是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离
是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离![]() (米)与该车的车速
(米)与该车的车速![]() (千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为
(千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为![]() ,在乙地的销售利润(单位:万元)为
,在乙地的销售利润(单位:万元)为![]() ,其中
,其中![]() 为销售量(单位:辆).
为销售量(单位:辆).
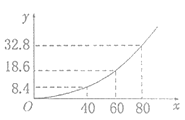
(1)若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润![]() 是多少?
是多少?
(2)如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为![]() ,
,![]() 为椭圆C的左右焦点,离心率为
为椭圆C的左右焦点,离心率为![]() ,短轴长为2。
,短轴长为2。
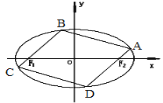
(1)求椭圆C的方程;
(2)如图,椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点![]() ,求该平行四边形ABCD面积的最大值.
,求该平行四边形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com