
【题目】下列叙述正确的是( )
A.命题“p且q”为真,则![]() 恰有一个为真命题
恰有一个为真命题
B.命题“已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件”
”的充分不必要条件”
C.命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]()
D.如果函数![]() 在区间
在区间![]() 上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有![]() ,那么函数
,那么函数![]() 在区间
在区间![]() 内有零点
内有零点
【答案】C
【解析】
由p且q的真值表,可判断正误;由充分必要条件的定义和特值法,可判断正误;由全称命题的否定为特称命题,可判断正误;由函数零点存在定理可判断正误.
解:对于A,命题“P且q为真,则P,q均为真命题”,故错误;
对于B,“a>b”推不出“a2>b2”,比如a=1,b=﹣1;反之也推不出,比如a=﹣2,b=0,“a>b”是“a2>b2”的不充分不必要条件,故错误;
对于C,命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]() ,故正确;
,故正确;
对于D,如果函数y=f(x)在区间[a,b]上是连续不断的一条曲线,
并且有f(a)f(b)<0,由零点存在定理可得函数y=f(x)在区间(a,b)内有零点,故错误.
其中真命题的个数为1,
故选:C.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
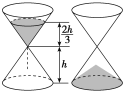
【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 、
、![]() 的定义域均为
的定义域均为![]() ,若对任意
,若对任意![]() ,且
,且![]() ,具有
,具有![]() ,则称函数
,则称函数![]() 为
为![]() 上的单调非减函数,给出以下命题:① 若
上的单调非减函数,给出以下命题:① 若![]() 关于点
关于点![]() 和直线
和直线![]() (
(![]() )对称,则
)对称,则![]() 为周期函数,且
为周期函数,且![]() 是
是![]() 的一个周期;② 若
的一个周期;② 若![]() 是周期函数,且关于直线
是周期函数,且关于直线![]() 对称,则
对称,则![]() 必关于无穷多条直线对称;③ 若
必关于无穷多条直线对称;③ 若![]() 是单调非减函数,且关于无穷多个点中心对称,则
是单调非减函数,且关于无穷多个点中心对称,则![]() 的图象是一条直线;④ 若
的图象是一条直线;④ 若![]() 是单调非减函数,且关于无穷多条平行于
是单调非减函数,且关于无穷多条平行于![]() 轴的直线对称,则
轴的直线对称,则![]() 是常值函数;以上命题中,所有真命题的序号是_________
是常值函数;以上命题中,所有真命题的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
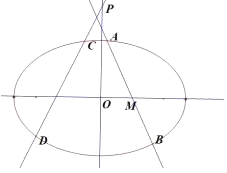
(1)求椭圆![]() 的方程;
的方程;
(2)如图,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() (点
(点![]() 在点
在点![]() 的上方),试求
的上方),试求![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,是否存在直线
,是否存在直线![]() (其中
(其中![]() ),使得
),使得![]() 到直线
到直线![]() 的距离
的距离![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com