
已知函数
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明 在
在 上是减函数;
上是减函数;
(3)函数 在
在 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
(1)详见解析;(2) 详见解析;(3) 函数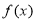 在
在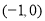 上是单调减函数.
上是单调减函数.
【解析】
试题分析:(1)首先看函数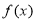 的定义域是否关于原点对称,再根据奇、偶函数的定义进行证明;(2)直接根据单调性的定义(取值—作差—变形—定号—判奇偶)进行证明即可;(3)由(2)的证明结果可知
的定义域是否关于原点对称,再根据奇、偶函数的定义进行证明;(2)直接根据单调性的定义(取值—作差—变形—定号—判奇偶)进行证明即可;(3)由(2)的证明结果可知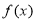 在
在 上的单调性,而
上的单调性,而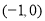 是
是 关于原点的对称区间,根据“奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反”直接做出判断.
关于原点的对称区间,根据“奇函数在对称区间上的单调性相同,偶函数在对称区间上的单调性相反”直接做出判断.
试题解析:(1)根据题意函数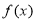 的定义域为:
的定义域为: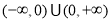 ,关于坐标原点对称.
,关于坐标原点对称.
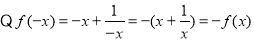 ,
, 在定义域上是奇函数.
在定义域上是奇函数.
(2) 设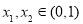 且
且 ,则
,则

 ,
, ,即
,即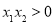 且
且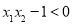 ;又
;又 ,
,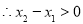 .
.
∴ ,即
,即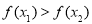
 函数
函数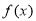 在
在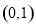 上是减函数.
上是减函数.
(3)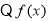 是奇函数且
是奇函数且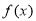 在
在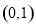 上是减函数;又
上是减函数;又
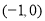 是
是 关于原点的对称区间.
关于原点的对称区间.
 在
在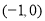 上是单调减函数.
上是单调减函数.
考点:1、函数奇偶性的证明;2、函数单调性的证明;3、奇、偶函数在对称区间上的单调性.


科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:选择题
设等差数列{ }{
}{  }的前n 项和为
}的前n 项和为 ,
, ,若
,若  ,则
,则  =
=
A.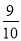 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第一次段考理数学卷(解析版) 题型:选择题
设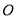 为坐标原点,点
为坐标原点,点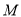 坐标为
坐标为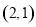 ,若
,若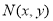 满足不等式组:
满足不等式组: ,则
,则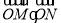 的最大值为
的最大值为


A.12 B.8 C.6 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期第一次月考数学试卷(解析版) 题型:选择题
已知集合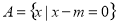 ,
, ,若
,若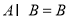 ,则
,则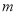 等于( )
等于( )
A.1 B.0或1 C.﹣1或1 D.0或1或﹣1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一9月月考数学试卷(解析版) 题型:选择题
设S,T,是R的两个非空子集,如果存在一个从S到T的函数 满足:
满足: 对任意
对任意 当
当 时,恒有
时,恒有 ,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是( )
,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是( )
A、
B、
C、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com