
分析 (1)对a分类讨论:a=0,解出即可判断出是否满足题意.a≠0时,A中至少有一个元素,满足△≥0,解得a范围即可得出.
(2)对a分类讨论:a=0,直接验证是否满足题意.a≠0时,由A中至多有一个元素,可得△≤0,解得a范围即可得出.
解答 解:(1)a=0,由-3x+2=0,解得x=$\frac{2}{3}$,满足题意,因此a=0.
a≠0时,∵A中至少有一个元素,∴△=9-8a≥0,解得a≤$\frac{9}{8}$,a≠0.
综上可得:a的取值范围是$(-∞,\frac{9}{8}]$.
(2)a=0,由-3x+2=0,解得x=$\frac{2}{3}$,满足题意,因此a=0.
a≠0时,∵A中至多有一个元素,∴△=9-8a≤0,解得a≥$\frac{9}{8}$.
综上可得:a的取值范围是{0}∪$[\frac{9}{8},+∞)$.
点评 本题考查了集合的性质、一元二次方程的实数根与判别式的关系,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 29 | C. | 37 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限的点集 | B. | 第二象限的点集 | C. | 第三象限的点集 | D. | 第四象限的点集 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 2015 | D. | -2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 型号A | 型号B | 型号C | |
| 高配性 | 10 | 20 | z |
| 低配型 | 30 | 50 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
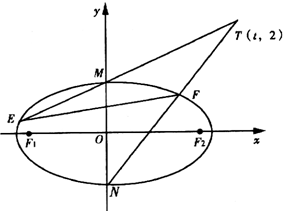 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,上顶点M,左、右焦点分别为F1,F2,△MF1F2的面积为$\sqrt{3}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,上顶点M,左、右焦点分别为F1,F2,△MF1F2的面积为$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com