练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在平面直角坐标系中，已知点A（-1，0），B（1，2），C（3，-1），点P（x，y）为△ABC边界及内部的任意一点，则x+y的最大值为3．

    分析 由三角形三个顶点的坐标作出平面区域，令z=x+y，化为y=-x+z，数形结合顶点最优解，把最优解的坐标代入得答案．

    解答 解：△ABC三个顶点坐标分别为A（-1，0），B（1，2），C（3，-1），
    如图，

    令z=x+y，化为y=-x+z，
    可知当直线y=-x+z过B时，直线在y轴上的截距最大，z有最大值为3．
    故答案为：3．

    点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

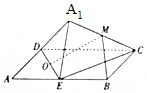    14．如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE（A1∉平面ABCD），若M、O分别为线段A1C、DE的中点，则在△ADE翻转过程中，下列说法错误的是（　　）
    A．与平面A1DE垂直的直线必与直线BM垂直
    B．异面直线BM与A1E所成角是定值
    C．一定存在某个位置，使DE⊥MO
    D．三棱锥A1-ADE外接球半径与棱AD的长之比为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=2|x-2|+3|x+3|．
    （1）解不等式：f（x）＞15；
    （2）若函数f（x）的最小值为m，正实数a，b满足4a+25b=m，证明：$\frac{1}{a}$+$\frac{1}{b}$≥$\frac{49}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知λ∈R，函数f（x）=ex-ex-λ（xlnx-x+1）的导数为g（x）．
    （1）求曲线y=f（x）在x=1处的切线方程；
    （2）若函数g（x）存在极值，求λ的取值范围；
    （3）若x≥1时，f（x）≥0恒成立，求λ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．从某市的中学生中随机调查了部分男生，获得了他们的身高数据，整理得到如下频率分布直方图．
    （Ⅰ）求a的值；
    （Ⅱ）假设同组中的每个数据用该组区间的中点值代替，估计该市中学生中的全体男生的平均身高；
    （Ⅲ）从该市的中学生中随机抽取一名男生，根据直方图中的信息，估计其身高在180cm 以上的概率．若从全市中学的男生（人数众多）中随机抽取3人，用X表示身高在180cm以上的男生人数，求随机变量X的分布列和数学期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

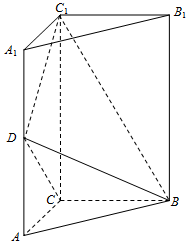    9．如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，∠ACB=90°，AC=BC=1，AA1=2，D是棱AA1的中点．   
    （Ⅰ）求证：B1C1∥平面BCD；
    （Ⅱ）求三棱锥B-C1CD的体积；
    （Ⅲ）在线段BD上是否存在点Q，使得CQ⊥BC1？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

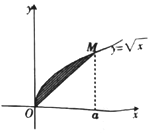    16．如图，点M在曲线y=$\sqrt{x}$，若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$，则实数a等于（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

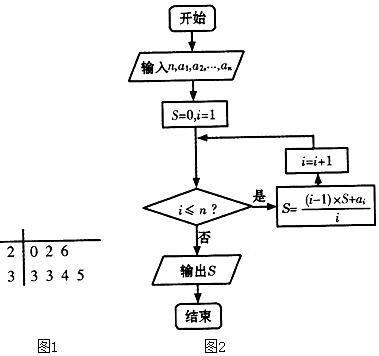
    13．某品牌洗衣机专柜在国庆期间举行促销活动，茎叶图1中记录了每天的销售量（单位：台），把这些数据经过如图2所示的程序框图处理后，输出的S=（　　）
    A．196B．203C．28D．29

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．平面内三点A，B，C满足|$\overrightarrow{BA}$|=3，|$\overrightarrow{BC}$|=4，$\overrightarrow{BA}$$•\overrightarrow{BC}$=0，M，N为平面内的动点，且$\overrightarrow{AM}$为单位向量，若$\overrightarrow{MC}$=2$\overrightarrow{MN}$，则|$\overrightarrow{BN}$|的最大值与最小值的和为（　　）
    A．10B．8C．7D．5

    查看答案和解析>>

    同步练习册答案