
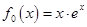 ,
,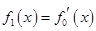 ,
,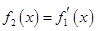 ,
,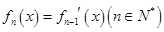 .
. 表达式(不需证明);
表达式(不需证明); 的极小值
的极小值 ;
;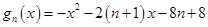 ,
,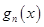 的最大值为
的最大值为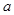 ,
, 的最小值为
的最小值为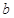 ,试求
,试求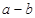 的最小值.
的最小值. ;(Ⅱ)
;(Ⅱ) 的极小值
的极小值 ;(Ⅲ)
;(Ⅲ)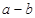 的最小值为
的最小值为 .
. ,
, 的表达式,观察式子的结构特征,用不完全归纳法归纳出
的表达式,观察式子的结构特征,用不完全归纳法归纳出 表达式(可以用数学归纳法给出证明);(Ⅱ)由(Ⅰ)知
表达式(可以用数学归纳法给出证明);(Ⅱ)由(Ⅰ)知 的表达式,要求极值点,就要借助
的表达式,要求极值点,就要借助 的导函数
的导函数 ,令
,令 ,解出可能的极值点,验证是极值后代入解析式,即可求出
,解出可能的极值点,验证是极值后代入解析式,即可求出 的最小值
的最小值 ;(Ⅲ)类比求函数
;(Ⅲ)类比求函数 的最小值的过程,即可求出函数
的最小值的过程,即可求出函数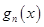 的极大值
的极大值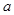 ,进而求出函数
,进而求出函数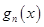 的最大值,从而得
的最大值,从而得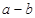 的关系式,将它看作数列,研究该数列相邻两项的关系,即可求得
的关系式,将它看作数列,研究该数列相邻两项的关系,即可求得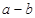 的最小值;得
的最小值;得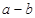 的关系式
的关系式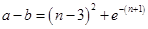 后,也可以构造函数
后,也可以构造函数 ,利用导数求它的最小值,即得
,利用导数求它的最小值,即得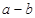 的最小值.
的最小值. 4分
4分 ,∴当
,∴当 时,
时, ;当
;当 时,
时, ,∴当
,∴当 时,
时, 取得极小值
取得极小值 ,即
,即 (
( ) 8分
) 8分 ,所以
,所以 . 9分
. 9分 ,∴
,∴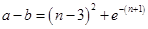 ,令
,令 ,则
,则 . 10分
. 10分 在
在 单调递增,∴
单调递增,∴ ,∵
,∵ ,
, ,
, 使得
使得 . 12分
. 12分 在
在 单调递增,∴当
单调递增,∴当 时,
时, ;当
;当 时,
时, ,即
,即 在
在 单调递增,在
单调递增,在 单调递减,∴
单调递减,∴ ,又∵
,又∵ ,
, ,
, ,
,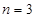 时,
时,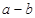 取得最小值
取得最小值 . 14分
. 14分 ,所以
,所以 . 9分
. 9分 ,∴
,∴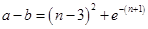 ,令
,令 ,则
,则 , 10分
, 10分 时,
时, ,又因为
,又因为 ,所以
,所以 ,
, ,
, ,
, ,所以
,所以 . 12分
. 12分 ,
, ,∴当
,∴当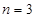 时,
时,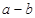 取得最小值
取得最小值 . 14分
. 14分

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
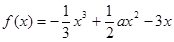 ,
,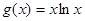
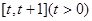 上的最小值;
上的最小值;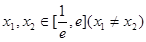 ,使方程
,使方程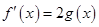
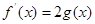 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
(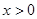 ,
,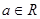 ),
),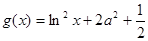 .
.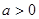 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数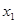 、
、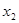 ,均有
,均有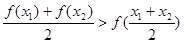 成立;
成立;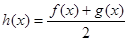 ,
, 在
在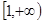 上单调递增,求实数
上单调递增,求实数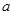 的取值范围;
的取值范围;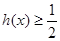 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com