
选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的
轴的
正半轴为极轴建立极坐标系,直线 过极坐标系内的两点
过极坐标系内的两点 和
和 .
.
(1)写出曲线 和直线
和直线 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(2)若 是曲线
是曲线 上任意一点,求
上任意一点,求 面积的最小值.
面积的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016届河北省邯郸市高三下第二次模拟考试数学(文)卷(解析版) 题型:解答题
已知函数 .
.
(1)设函数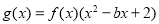 .当
.当 时,若函数
时,若函数 有极值,求实数
有极值,求实数 的取值范围;
的取值范围;
(2)若 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016届河北省邯郸市高三下第二次模拟考试数学(理)卷(解析版) 题型:选择题
已知向量 与
与 的夹角为60°,
的夹角为60°, ,
, ,则
,则 在
在 方向上的投影为( )
方向上的投影为( )
A. B.2 C.
B.2 C.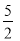 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2016届广东省湛江市普通高考测试卷(二)理科数学试卷(解析版) 题型:选择题
设数列 为等差数列,
为等差数列, 为等比数列.若
为等比数列.若 ,且
,且 ,则数列
,则数列
 的公比为( )
的公比为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届广东省湛江市普通高考测试卷(二)理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入 ,则输出
,则输出 的值为( )
的值为( )

A.2 B.5 C.11 D.23
查看答案和解析>>
科目:高中数学 来源:2016届广东省深圳市高三第二次调研考试数学(文)试卷(解析版) 题型:解答题
2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随机抽取了年龄在 岁之间的100人进行调查,并按年龄绘制的频率分布直方图如下图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制的频率分布直方图如下图所示,其分组区间为: .把年龄落在区间
.把年龄落在区间 和
和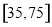 内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为9:11.
内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”与“中老年人”的人数之比为9:11.

(1)求图中 的值;
的值;
(2)若“青少年人”中有15人在关注两会,根据已知条件完成下面的 列联表,根据此统计结果能否
列联表,根据此统计结果能否
有99%的把握认为“中老年人”比“青少年人”更加关注两会?
关注 | 不关注 | 合计 | |
青少年人 | 15 | ||
中老年人 | |||
合计 | 50 | 50 | 100 |
附参考公式: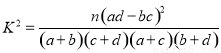 ,其中
,其中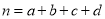 .
.
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2016届广东省深圳市高三第二次调研考试数学(文)试卷(解析版) 题型:选择题
如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体
外接球的表面积为( )

A. B.
B. C.
C.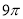 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届广东省深圳市高三第二次调研考试数学(理)试卷(解析版) 题型:解答题
某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80
分为“优秀”,小于60分为“不合格”,其它为“合格”.
(1)某校高一年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽
样的方法从高一学生中抽取了45名学生的综合素质评价结果,其各个等级的频数统计如下表:
等级 | 优秀 | 合格 | 不合格 |
男生(人) | 15 |
| 5 |
女生(人) | 15 | 3 |
|
根据表中统计的数据填写下面 列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优
列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优
秀与性别有关”?
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
(2)以(1)中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名
学生是否“优秀”相互独立,现从该市高一学生中随机抽取3人.
①求所选3人中恰有2人综合素质评价为“优秀”的概率;
②记 表示这3人中综合素质评价等级为“优秀”的个数,求
表示这3人中综合素质评价等级为“优秀”的个数,求 的数学期望.
的数学期望.
参考公式: ,其中
,其中 .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com