
【题目】如图,正方形ABCD的边长为1,P、Q分别为边AB、DA上的点,当△APQ的周长为2时,求∠PCQ的大小. 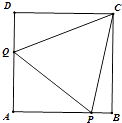
【答案】解:设AQ=x,AP=y,则DQ=1﹣x,PB=1﹣y,(0<x<1,0<y<1),
则tan∠DCQ= ![]() =1﹣x,tan∠BCP=1﹣y,tan(∠DCQ+∠BCP)=
=1﹣x,tan∠BCP=1﹣y,tan(∠DCQ+∠BCP)= ![]() =
= ![]() ①.
①.
在Rt△APQ中,PQ2=AQ2+AP2=x2+y2 , 又PQ=2﹣(x+y),∴(2﹣x﹣y)2=x2+y2 , 即 xy=2(x+y)﹣2 ②.
把②代入①可得tan(∠DCQ+∠BCP)=1,∴∠DCQ+∠BCP=45°,∴∠PCQ=45°
【解析】设AQ=x,AP=y,利用直角三角形中的边角关系求得tan∠DCQ= ![]() =1﹣x,tan∠BCP=1﹣y,再两角和的正切公式求得tan(∠DCQ+∠BCP)=1,可得∠DCQ+∠BCP=45°,从而求得∠PCQ=45°.
=1﹣x,tan∠BCP=1﹣y,再两角和的正切公式求得tan(∠DCQ+∠BCP)=1,可得∠DCQ+∠BCP=45°,从而求得∠PCQ=45°.
【考点精析】通过灵活运用两角和与差的正切公式,掌握两角和与差的正切公式:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①已知a,b,m都是正数,并且a<b,则 ![]() >
> ![]() ;
;
②在△ABC中,角A,B,C的对边分别为a,b,c,若∠A=60°,a=7,b=8,则三角形有一解;
③若函数f(x)= ![]() ,则f(
,则f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )=5;
)=5;
④在等比数列{an}中,a1+a2+…+an= ![]() (其中n∈N* , q为公比);
(其中n∈N* , q为公比);
⑤如图,在正方体ABCD﹣A1B1C1D1中,点M,N分别是CD,CC1的中点,则异面直线A1M与DN所成角的大小是90°.
其中真命题有(写出所有真命题的序号).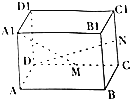
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD中, 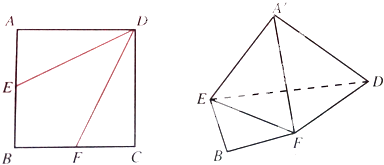
(1)点E是AB的中点,点F是BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.求证:A′D⊥EF
(2)当BE=BF= ![]() BC时,求三棱锥A′﹣EFD的体积.
BC时,求三棱锥A′﹣EFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点 ,
两点 , ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() (不与坐标轴垂直)与椭圆交于
(不与坐标轴垂直)与椭圆交于![]() 两点,若在线段
两点,若在线段![]() 上存在点
上存在点![]() ,
,
使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1CAC1
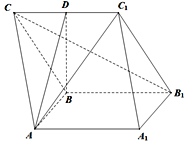
(Ⅰ)求证:平面AA1B1B面BB1C1C;
(Ⅱ)若D是CC1中点,ADB是二面角A-CC1-B的平面角,求直线AC1与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 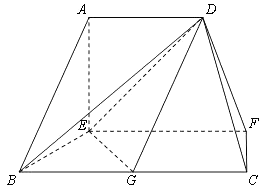
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com