
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() ,
,![]() 为椭圆
为椭圆![]() 的左焦点,椭圆的利息率为
的左焦点,椭圆的利息率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交抛物线
并延长其交抛物线![]() 于点
于点![]() ,
,![]() 为抛物线
为抛物线![]() 上一动点,且在
上一动点,且在![]() ,
,![]() 之间移动.
之间移动.

(1)当![]() 取最小值时,求
取最小值时,求![]() 的值;
的值;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 的面积取最大值时,求面积最大值及此时直线
的面积取最大值时,求面积最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() ;
;![]()
【解析】
(1)用![]() 表示出
表示出![]() ,
,![]() ,根据基本不等式得出
,根据基本不等式得出![]() 的值,从而得出
的值,从而得出![]() 和
和![]() 的方程;
的方程;
(2)用![]() 表示出椭圆方程,联立方程组得出
表示出椭圆方程,联立方程组得出![]() 点坐标,计算出△
点坐标,计算出△![]() 的三边关于
的三边关于![]() 的式子,从而确定
的式子,从而确定![]() 的值,求出
的值,求出![]() 的距离和
的距离和![]() 到直线
到直线![]() 的距离,利用二次函数性质得出
的距离,利用二次函数性质得出![]() 面积的最大值,即可求得直线
面积的最大值,即可求得直线![]() 的方程.
的方程.
解:(1)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以当![]() 取最小值时,
取最小值时,![]() ,又因为
,又因为![]() ,所以
,所以![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,设椭圆的标准方程为
,设椭圆的标准方程为![]() .
.
设![]() ,
,![]() ,由
,由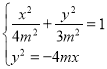 得
得![]() ,所以
,所以![]() 或
或![]() (舍去),代入抛物线方程得
(舍去),代入抛物线方程得![]() ,即
,即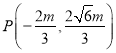 ,
,
于是![]() ,
,![]() ,
,![]() ,又因为
,又因为![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以![]() .此时抛物线方程为
.此时抛物线方程为![]() ,
,![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .联立
.联立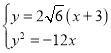 ,得
,得![]() 或
或![]() (舍去),于是
(舍去),于是![]() ,所以
,所以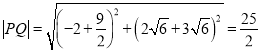 ,
,
设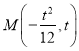 (
(![]() )到直线
)到直线![]() 的距离为
的距离为![]() ,则
,则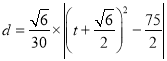 ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 的面积的最大值为
的面积的最大值为![]() .此时
.此时![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组样本点![]() ,其中
,其中![]() .根据最小二乘法求得的回归方程是
.根据最小二乘法求得的回归方程是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 若所有样本点都在![]() 上,则变量间的相关系数为1
上,则变量间的相关系数为1
B. 至少有一个样本点落在回归直线![]() 上
上
C. 对所有的预报变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差
有误差
D. 若![]() 斜率
斜率![]() ,则变量
,则变量![]() 与
与![]() 正相关
正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉持“绿水青山就是金山银山”的生态文明发展理念,为推动新能源汽车产业迅速发展,有必要调查研究新能源汽车市场的生产与销售.下图是我国某地区![]() 年至
年至![]() 年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
年新能源汽车的销量(单位:万台)按季度(一年四个季度)统计制成的频率分布直方图.
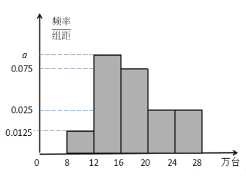
(1)求直方图中![]() 的值,并估计销量的中位数;
的值,并估计销量的中位数;
(2)请根据频率分布直方图估计新能源汽车平均每个季度的销售量(同一组数据用该组中间值代表),并以此预计![]() 年的销售量.
年的销售量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形纸片![]() 的边
的边![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() 与
与![]() 上,现将纸片的右下角沿
上,现将纸片的右下角沿![]() 翻折,使得顶点
翻折,使得顶点![]() 翻折后的新位置
翻折后的新位置![]() 恰好落在边
恰好落在边![]() 上,设
上,设![]() .
.
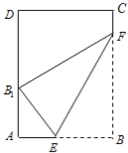
(1)若![]() ,求
,求![]() 的长.
的长.
(2)设![]() ,将
,将![]() 的长度表示为关于
的长度表示为关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com