练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱柱中，侧面为棱长为2的菱形，，，．

    （1）求证：面面；

    （2）求直线与面所成角．

    【答案】（1）见解析（2）．

    【解析】

    （1）连结交于点，连结，通过菱形的性质得出，，得出为等边三角形，根据三边关系得出，则，而，根据线面垂直的判定定理得出平面，而平面，从而可证出平面平面；

    （2）由面面垂直的性质得出面，则即为与面所成角，通过几何法求得，即可求出直线与面所成角．

    解：（1）证明：连结交于点，连结，

    因为为菱形，，

    所以，，

    则为等边三角形，即可得，

    又，

    所以在中，，

    ∴，即，

    又知，，

    且平面，平面，

    所以平面，平面，

    即平面平面.

    （2）由（1）知平面平面，

    因为，平面平面，

    所以面，

    则即为与面所成角，

    在中，，，

    ∴，

    ∴，

    所以直线与面所成角为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥P﹣ABCD中，PC⊥底面ABCD，PC＝CD＝2，E为AB的中点，底面四边形ABCD满足∠ADC＝∠DCB＝90°，AD＝1，BC＝3．

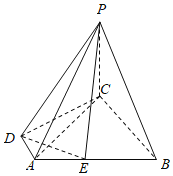
    （Ⅰ）求证：平面PDE⊥平面PAC；

    （Ⅱ）求直线PC与平面PDE所成角的正弦值；

    （Ⅲ）求二面角D﹣PE﹣B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为纪念“五四运动”100周年，某校团委举办了中国共产主义青年团知识宣讲活动活动结束后，校团委对甲、乙两组各10名团员进行志愿服务次数调查，次数统计结果用茎叶图记录如下，乙组记录中有一个数据模糊，无法确认，在图中以表示．

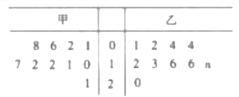
    （1）若甲组服务次数的平均值不小于乙组服务次数的平均值，求图中所有可能的取值；

    （2）团委决定对甲、乙两组中服务次数超过15次的团员授予“优秀志愿者”称号设，现从所有“优秀志愿者”里任取3人，求其中乙组的人数的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年4月，北京世界园艺博览会开幕，为了保障园艺博览会安全顺利地进行，某部门将5个安保小组全部安排到指定的三个不同区域内值勤，则每个区域至少有一个安保小组的排法有（ ）

    A.150种B.240种C.300种D.360种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若关于某设备的使用年限（年）和所支出的维修费（万元）有如下统计资料：

    若由资料知，对呈线性相关关系．

    （1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （2）估计使用年限为10年时，维修费用约是多少？（精确到两位小数）；

    （3）计算第2年和第6年的残差.

    附：回归直线的斜率和截距的最小二乘估计分别为；.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车站每天上午发出两班客车，每班客车发车时刻和发车概率如下：第一班车：在8:00，8:20，8:40发车的概率分别为，，；第二班车：在9:00，9:20，9:40发车的概率分别为，，．两班车发车时刻是相互独立的，一位旅客8:10到达车站乘车．求：

    （1）该旅客乘第一班车的概率；

    （2）该旅客候车时间（单位：分钟）的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，设抛物线的准线与轴交于椭圆的右焦点，为椭圆的左焦点，椭圆的利息率为，抛物线与椭圆交于轴上方一点，连接并延长其交抛物线于点，为抛物线上一动点，且在，之间移动.

    （1）当取最小值时，求的值；

    （2）若的边长恰好是三个连续的自然数，当的面积取最大值时，求面积最大值及此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，图中点A表示甲的创造力指标值为4，点B表示乙的空间能力指标值为3，则下面叙述正确的是

    A. 乙的记忆能力优于甲的记忆能力

    B. 乙的创造力优于观察能力

    C. 甲的六大能力整体水平优于乙

    D. 甲的六大能力中记忆能力最差

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着中美贸易战的不断升级，越来越多的国内科技巨头加大了科技研发投入的力度．中华技术有限公司拟对“麒麟”手机芯片进行科技升级，根据市场调研与模拟，得到科技升级投入x（亿元与科技升级直接收益y（亿元）的数据统计如下：

    序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    x

    2

    3

    4

    6

    8

    10

    13

    21

    22

    23

    24

    25

    y

    13

    22

    31

    42

    50

    56

    58

    68.5

    68

    67.5

    66

    66

    当时，建立了y与x的两个回归模型：模型①：；模型②：；当时，确定y与x满足的线性回归方程为．

    （1）根据下列表格中的数据，比较当时模型①、②的相关指数的大小，并选择拟合精度更高、更可靠的模型，预测对“麒麟”手机芯片科技升级的投入为17亿元时的直接收益．

    回归模型

    模型①

    模型②

    回归方程

    182.4

    79.2

    （附：刻画回归效果的相关指数，）

    （2）为鼓励科技创新，当科技升级的投入不少于20亿元时，国家给予公司补贴5亿元，以回归方程为预测依据，比较科技升级投入17亿元与20亿元时公司实际收益的大小．

    （附：用最小二乘法求线性回归方程的系数：，）

    （3）科技升级后，“麒麟”芯片的效率X大幅提高，经实际试验得X大致服从正态分布．公司对科技升级团队的奖励方案如下：若芯片的效率不超过50%，不予奖励：若芯片的效率超过50%，但不超过53%，每部芯片奖励2元；若芯片的效率超过53%，每部芯片奖励4元记为每部芯片获得的奖励，求（精确到0.01）．

    （附：若随机变量，则，）

    查看答案和解析>>

    同步练习册答案