
【题目】若关于某设备的使用年限![]() (年)和所支出的维修费
(年)和所支出的维修费![]() (万元)有如下统计资料:
(万元)有如下统计资料:

若由资料知,![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)估计使用年限为10年时,维修费用约是多少?(精确到两位小数);
(3)计算第2年和第6年的残差.
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
科目:高中数学 来源: 题型:
【题目】为参与某次救援,潜水员需潜至水下30米处进行作业.在下潜与返回水面的过程中保持匀速,速度均为![]() 米/分钟(
米/分钟(![]() ,
,![]() 为常数),下潜过程中每分钟耗氧量与速度
为常数),下潜过程中每分钟耗氧量与速度![]() 的平方成正比,当速度为1米/分钟时,每分钟耗氧量为0.2升;在水下30米作业时,每分钟耗氧量为0.4升:返回水面的过程中每分钟耗氧量为0.2升假定氧气瓶中氧气为20升,潜水员下潜时开始使用氧气瓶中的氧气,返回到水面时氧气瓶中氧气恰好用尽.
的平方成正比,当速度为1米/分钟时,每分钟耗氧量为0.2升;在水下30米作业时,每分钟耗氧量为0.4升:返回水面的过程中每分钟耗氧量为0.2升假定氧气瓶中氧气为20升,潜水员下潜时开始使用氧气瓶中的氧气,返回到水面时氧气瓶中氧气恰好用尽.
(1)试求潜水员在水下30米作业的时间![]() (单位:分钟)与速度
(单位:分钟)与速度![]() 的函数解析式;
的函数解析式;
(2)试求潜水员在水下30米能作业的最长时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年![]() 市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于2018年
市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于2018年![]() 市入选中国空气优良城市
市入选中国空气优良城市![]() .已知该市设有9个监测站用于监测空气质量指数(
.已知该市设有9个监测站用于监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,4,3个监测站,并以9个监测站测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,4,3个监测站,并以9个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为119,已知轻度污染区
为119,已知轻度污染区![]() 平均值为70,中度污染区
平均值为70,中度污染区![]() 平均值为115,求重度污染区
平均值为115,求重度污染区![]() 平均值;
平均值;
(2)如图是2018年11月份30天的![]() 的频率分布直方图,11月份仅有1天
的频率分布直方图,11月份仅有1天![]() 在
在![]() 内.
内.
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于150就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
小于150就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从11月份![]() 不小于170的数据中抽取三天的数据进行研究,求抽取的这三天中
不小于170的数据中抽取三天的数据进行研究,求抽取的这三天中![]() 值不小于200的天数的分布列和数学期望.
值不小于200的天数的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组样本点![]() ,其中
,其中![]() .根据最小二乘法求得的回归方程是
.根据最小二乘法求得的回归方程是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 若所有样本点都在![]() 上,则变量间的相关系数为1
上,则变量间的相关系数为1
B. 至少有一个样本点落在回归直线![]() 上
上
C. 对所有的预报变量![]() ,
,![]() 的值一定与
的值一定与![]() 有误差
有误差
D. 若![]() 斜率
斜率![]() ,则变量
,则变量![]() 与
与![]() 正相关
正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: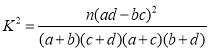 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com