
已知函数f(x)=asin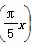 +btan
+btan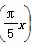 (a,b为常数,x∈R).若f(1)=1,则不等式f(31)>log2x的解集为________.
(a,b为常数,x∈R).若f(1)=1,则不等式f(31)>log2x的解集为________.
科目:高中数学 来源: 题型:
连续抛掷两枚正方体骰子(它们的六个面分别标有数字1,2,3,4,5,6),记所得朝上的面的点数分别为x,y,过坐标原点和点P(x,y)的直线的倾斜角为θ,则θ>60°的概率为( )
A.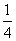 B.
B.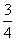 C.
C.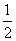 D.
D.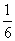
查看答案和解析>>
科目:高中数学 来源: 题型:
据市场调查,某种商品一年中12个月的价格与月份的关系可以近似地用函数f(x)=Asin(ωx+φ)+7(A>0,ω>0,|φ|< )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
A.4.2万元 B.5.6万元
C. 7万元 D.8.4万元
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2sin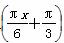 (0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图象上的最高点和最低点.
(1)求点A、B的坐标以及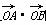 的值;
的值;
(2)设点A、B分别在角α、β的终边上,求tan(α-2β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线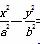 =1(a>0,b>0)的一个焦点与抛物线y2=4
=1(a>0,b>0)的一个焦点与抛物线y2=4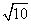 x的焦点重合,且双曲线的离心率等于
x的焦点重合,且双曲线的离心率等于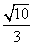 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A.x2-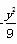 =1 B.x2-y2=15
=1 B.x2-y2=15
C. 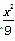 -y2=1 D.
-y2=1 D. 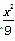 -
-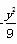 =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com