练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．直线3x+y+2=0的倾斜角为π-arctan3．

    分析 根据题意，设直线3x+y+2=0的倾斜角为θ，求出直线的斜率，即可得tanθ=-3，由反三角函数的定义即可得答案．

    解答 解：根据题意，设直线3x+y+2=0的倾斜角为θ，
    直线3x+y+2=0的斜率k=-3，
    则有tanθ=-3，
    又由0≤θ＜π，
    则θ=π-arctan3；
    故答案为：π-arctan3．

    点评 本题考查直线的倾斜角，涉及反三角函数的应用，关键是求出直线的斜率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．证明下列不等式：
    （1）$\sqrt{6}$+$\sqrt{7}$＞$2\sqrt{2}+\sqrt{5}$            
    （2）${a}^{2}+{b}^{2}+3≥ab+\sqrt{3}（a+b）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设函数f（x）=x3+ax2+bx+5，曲线y=f（x）在点（1，f（1））处的切线方程为y=3x+1．
    （1）求f（x）的表达式；
    （2）求y=f（x）在[-3，1]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

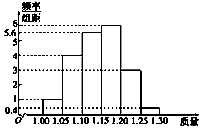    4．为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
    （1）在下面表格中填写相应的频率；
    分组频率
    [1.00，1.05）
    [1.05，1.10）
    [1.10，1.15）
    [1.15，1.20）
    [1.20，1.25）
    [1.25，1.30）
    （2）估计数据落在[1.15，1.30）中的概率为多少；
    （3）将上面捕捞的100条鱼分别作一记号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．原命题：“设a，b，c∈R，若a＞b，则ac2＞bc2”，在原命题以及它的逆命题、否命题、逆否命题中，真命题的个数为（　　）
    A．0B．1C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知关于x的方程$\sqrt{1-{x^2}}$+x+m=0有两个不等实数根，则实数m的取值范围（-$\sqrt{2}$，-1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．某校高一年级有甲、乙、丙三位学生，他们第一次、第二次、第三次月考的物理成绩如表：
     第一次月考物理成绩第二次月考物理成绩第三次月考物理成绩
    学生甲 80 85 90
    学生乙 81 83 85
    学生丙 90 86 82
    则下列结论正确的是（　　）
    A．甲、乙、丙第三次月考物理成绩的平均数为86
    B．在这三次月考物理成绩中，甲的成绩平均分最高
    C．在这三次月考物理成绩中，乙的成绩最稳定
    D．在这三次月考物理成绩中，丙的成绩方差最大

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在极坐标系中，直线l的极坐标方程为ρcos（θ+$\frac{π}{3}$）=1．以极点O为原点，极轴为x轴的正半轴建立平面直角坐标系，圆C的参数方程为$\left\{\begin{array}{l}{x=rcosθ}\\{y=rsinθ}\end{array}\right.$（θ为参数）．若直线l与圆C相切，求r的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知定义在R上的奇函数f（x）满足f（x-4）=-f（x），且在区间[0，2]上是增函数，若方程f（x）=m（m＞0）在区间[-8，8]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4=-8．

    查看答案和解析>>

    同步练习册答案