
| A. | m≤2 | B. | m<2 | C. | m≤3 | D. | m<3 |
分析 由配方法化简x2+x+1,将分式不等式等价转化为3x2+2x+2≥m(x2+x+1),化简后由恒成立问题和二次函数的性质列出不等式组,求出实数m的取值范围.
解答 解:∵x2+x+1=${(x+\frac{1}{2})}^{2}+\frac{3}{4}>0$恒成立,
∴不等式$\frac{3{x}^{2}+2x+2}{{x}^{2}+x+1}$≥m等价于3x2+2x+2≥m(x2+x+1),
即(3-m)x2+(2-m)x+2-m≥0对任意实数x都成立,
①当3-m=0,即m=3时,不等式为-x-1≥0,对任意实数x恒不成立;
②当3-m≠0,即m≠3时,
有$\left\{\begin{array}{l}{3-m>0}\\{(2-m)^{2}-4×(3-m)×(2-m)≤0}\end{array}\right.$,解得m≤2,
综上可得,实数m的取值范围是(-∞,2],
故选:A.
点评 本题考查了分式不等式的等价转化与解法,一元二次不等式的解法,以及一元二次函数的性质,考查分类讨论思想、转化思想,化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.
如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 焦虑 | 说谎 | 懒惰 | 总计 | |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 65 | 110 |
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在α内必存在与a平行的直线,不一定存在与a垂直的直线 | |
| B. | 在α内不一定存在与a平行的直线,必存在与a垂直的直线 | |
| C. | 在α内必存在与a平行的直线.必存在与a垂直的直线 | |
| D. | 在α内不一定存在与a平行的直线.不-定存在与a垂直的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
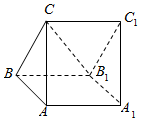 如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<$\frac{1}{3}$ | B. | 0<m≤$\frac{1}{3}$ | C. | $\frac{1}{3}$<m<1 | D. | $\frac{1}{3}$<m≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com