
分析 求出直线的普通方程,利用点到直线的距离公式,通过三角函数的有界性求解最小值.
解答 解:直线 l:$\left\{\begin{array}{l}{x=3+\frac{\sqrt{2}}{2}t}\\{y=-3+\frac{\sqrt{2}}{2}t}\\{\;}\end{array}\right.$(t为参数),的普通方程为:x-y-6=0.
P到直线l距离为:$\frac{|4cosθ-3sinθ-6|}{\sqrt{2}}$=$\frac{|5cos(θ+α)-6|}{\sqrt{2}}$,其中tanα=$\frac{3}{4}$.
当cos(θ+α)=1时,表达式取得最小值:$\frac{\sqrt{2}}{2}$.
点评 本题考查点到直线的距离公式以及参数方程的应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | {0,1} | C. | (-1,$\sqrt{e}$] | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
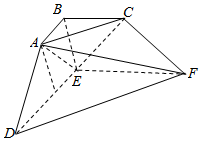 如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.
如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$-1 | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{-\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
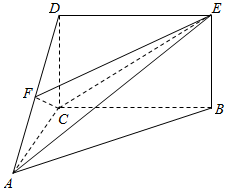 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 2 | C. | 1或0 | D. | 0或1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤2 | B. | m<2 | C. | m≤3 | D. | m<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com