
| A. | 1或2 | B. | 2 | C. | 1或0 | D. | 0或1或2 |
分析 可采用特殊值的方法,通过排除法得出答案.
解答 解:f(x)=$\frac{1}{2}$x2-|x-2a|有3个或4个零点,
∴$\frac{1}{2}$x2=|x-2a|,
∴x2-2x+4a=0和x2+2x-4a=0,
当a=0时,有三个根,符合题意,代入g(x)=4ax2+2x+1=2x+1有一个零点,排除B;
取a=$\frac{1}{8}$,有四个根,符合题意,代入g(x)=4ax2+2x+1=$\frac{1}{2}$x2+2x+1有两个零点;
若g(x)=4ax2+2x+1没有零点,则a>1,
x2-2x+4a=0没有根,不符合题意,故g(x)=4ax2+2x+1一定有零点,
故选A.
点评 考查了函数零点的概念和对问题的转化思想.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
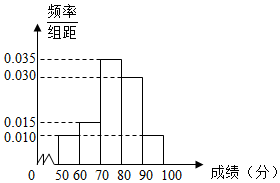 如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )
如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )| A. | 30 | B. | 25 | C. | 22 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8+5$\sqrt{3}$ | B. | 4+5$\sqrt{3}$ | C. | 12 | D. | 4+5$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 焦虑 | 说谎 | 懒惰 | 总计 | |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 65 | 110 |
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在α内必存在与a平行的直线,不一定存在与a垂直的直线 | |
| B. | 在α内不一定存在与a平行的直线,必存在与a垂直的直线 | |
| C. | 在α内必存在与a平行的直线.必存在与a垂直的直线 | |
| D. | 在α内不一定存在与a平行的直线.不-定存在与a垂直的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
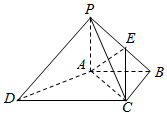 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,CD=2,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,AB⊥BC,AB=BC=PA=1,CD=2,点E在棱PB上,且PE=2EB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com