
| A. | 8+5$\sqrt{3}$ | B. | 4+5$\sqrt{3}$ | C. | 12 | D. | 4+5$\sqrt{3}$ |
分析 由诱导公式、两角和的余弦公式化简已知的式子,由内角的范围、商的关系、特殊角的三角函数值求出B,结合条件判断出△ABC为等边三角形,∠AOB=θ边求出θ的范围,利用三角形的面积公式与余弦定理,表示出得SOACB,利用辅助角公式化简,由θ的范围和正弦函数的性质求出平面四边形OACB面积的最大值.
解答  解:∵cosC+(cosA-$\sqrt{3}$sinA)cosB=0,cosC=-cos(A+B),
解:∵cosC+(cosA-$\sqrt{3}$sinA)cosB=0,cosC=-cos(A+B),
∴cosAcosB-$\sqrt{3}$sinAcosB=cos(A+B)=cosAcosB-sinAsinB,
化简得$\sqrt{3}$sinAcosB=sinAsinB,
∵A为三角形内角,sinA≠0,∴tanB=$\sqrt{3}$,
∴由B∈(0,π)得,B=$\frac{π}{3}$,
又∵a=c,∴△ABC为等边三角形;
设∠AOB=θ,则0<θ<π,
∴SOACB=S△AOB+S△ABC=$\frac{1}{2}$|OA|•|OB|sinθ+$\frac{1}{2}$×|AB|2×$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$×4×2×sinθ+$\frac{\sqrt{3}}{4}$(|OA|2+|OB|2-2|OA|•|OB|cosθ)
=4sinθ+$\frac{\sqrt{3}}{4}$(4+16-2×2×4×cosθ)=4sinθ-4$\sqrt{3}$cosθ+5$\sqrt{3}$
=8sin(θ-$\frac{π}{3}$)+5$\sqrt{3}$,
∵0<θ<π,∴-$\frac{π}{3}$<θ-$\frac{π}{3}$<$\frac{2π}{3}$,
∴当θ-$\frac{π}{3}$=$\frac{π}{2}$,即θ=$\frac{5π}{6}$时,sin(θ-$\frac{π}{3}$)取得最大值1,
∴平面四边形OACB面积的最大值为8+5$\sqrt{3}$.
故选A.
点评 本题考查三角函数中的恒等变换中的公式,余弦定理的应用,考查化简、变形及运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
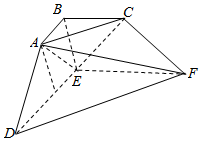 如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.
如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
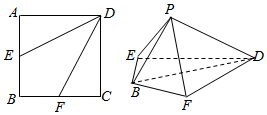 如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$-1 | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{-\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
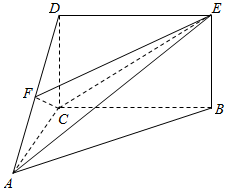 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 2 | C. | 1或0 | D. | 0或1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com