
分析 (Ⅰ)设动点P坐标为(x,y),利用两点间的距离公式列出曲线C的方程即可;
(Ⅱ)利用点到直线的距离公式表示出圆心到直线y=kx+1的距离d,根据$\overrightarrow{DA}$⊥$\overrightarrow{DB}$,且两向量的模为半径,求出d的值,进而求出k与|$\overrightarrow{AB}$|的值即可.
解答 解:(Ⅰ)设动点P的坐标为(x,y),
根据题意得:$\sqrt{(x-2)^{2}+(y-3)^{2}}$=4,
整理得:(x-2)2+(y-3)2=16,
则曲线C的方程为(x-2)2+(y-3)2=16;
(Ⅱ)圆心(2,3)到直线y=kx+1的距离d=$\frac{|2k-2|}{\sqrt{{k}^{2}+1}}$,
∵$\overrightarrow{DA}$⊥$\overrightarrow{DB}$,|$\overrightarrow{DA}$|=|$\overrightarrow{DB}$|=r=4,
∴d=$\frac{1}{2}$|AB|=$\frac{\sqrt{2}}{2}$r=$\frac{\sqrt{2}}{2}$×4=2$\sqrt{2}$,
∴$\frac{|2k-2|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,
解得:k=-1,|$\overrightarrow{AB}$|=4$\sqrt{2}$,
则当k=-1时,$\overrightarrow{DA}$⊥$\overrightarrow{DB}$,此时|$\overrightarrow{AB}$|=4$\sqrt{2}$.
点评 此题考查了直线与圆的位置关系,以及轨迹方程,熟练掌握公式及法则是解本题的关键.


科目:高中数学 来源: 题型:解答题
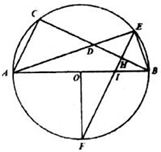 如图,AB是圆O的直径,点D是弦BC的中点,直线AD交圆O于点E,过点E作EF⊥BC于点H,交圆O于点F,交AB于点I,若OF⊥AB.
如图,AB是圆O的直径,点D是弦BC的中点,直线AD交圆O于点E,过点E作EF⊥BC于点H,交圆O于点F,交AB于点I,若OF⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
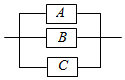 如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )
如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )| A. | 0.504 | B. | 0.994 | C. | 0.496 | D. | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
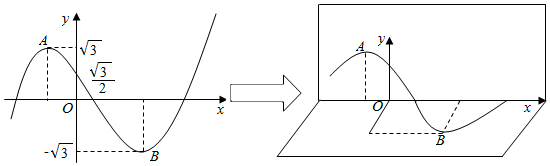
| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | |||
| Asin(ωx+φ) | 0 | 2 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
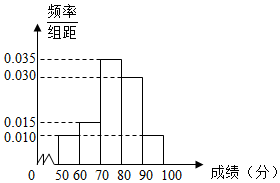 如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )
如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )| A. | 30 | B. | 25 | C. | 22 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8+5$\sqrt{3}$ | B. | 4+5$\sqrt{3}$ | C. | 12 | D. | 4+5$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com