
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | |||
| Asin(ωx+φ) | 0 | 2 | -2 | 0 |
分析 (1)根据用五点法作函数y=Asin(ωx+φ)在一个周期上的图象的方法,将上表数据补充完整,直接写出函数f(x)的解析式.
(2)令t=2x+$\frac{π}{3}$,可求t∈[-$\frac{2π}{3}$,$\frac{2π}{3}$],并做出函数y=2|sint|的图象,利用正弦函数的图象和性质,结合有两个交点数形结合即可得解m的取值范围.
解答 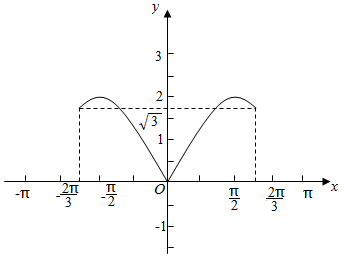 解:(1)根据表中已知数据可得:A=2,$\frac{π}{12}$ω+φ=$\frac{π}{2}$,$\frac{7π}{12}$ω+φ=$\frac{3π}{2}$,
解:(1)根据表中已知数据可得:A=2,$\frac{π}{12}$ω+φ=$\frac{π}{2}$,$\frac{7π}{12}$ω+φ=$\frac{3π}{2}$,
解得ω=2,φ=$\frac{π}{3}$,数据补全如下表:
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| Asin(φx+φ) | 0 | 2 | 0 | -2 | 0 |
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,考查了作图能力和数形结合思想,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是圆O的内接四边形,其中AB=AC,∠ABD=∠CBD,AC与BD交于点F,直线BC与AD交于点E.
如图,四边形ABCD是圆O的内接四边形,其中AB=AC,∠ABD=∠CBD,AC与BD交于点F,直线BC与AD交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | {0,1} | C. | (-1,$\sqrt{e}$] | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
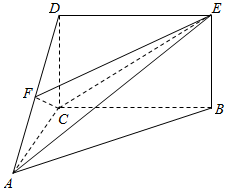 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com