
分析 根据河西不等式可直接求解.
解答 解:(1)由柯西不等式:[x2+(2y)2+(3z)2][12+( $\frac{1}{2}$)2+( $\frac{1}{3}$)2]≥(x+$\frac{1}{2}$×2y+$\frac{1}{3}$×3z)2,
∴$\frac{49}{36}$a≥(x+y+z)2(a>0),
∴-$\frac{7}{6}$$\sqrt{a}$≤x+y+z≤$\frac{7}{6}$$\sqrt{a}$
∵x+y+z的最大值是1,
∴$\frac{7}{6}$$\sqrt{a}$=1,得a=$\frac{36}{49}$;
(2)由柯西不等式:[x2+($\sqrt{2}$y)2+($\sqrt{3}$z)2][32+( $\sqrt{2}$)2+( $\frac{\sqrt{3}}{3}$)2]≥(3x+2y+z)2,
∴12≥(3x+2y+z)2,
∴-2$\sqrt{3}$≤3x+2y+z≤2$\sqrt{3}$
∴3x+2y+z的最小值是-2$\sqrt{3}$.
点评 考查了柯西不等式的应用,难点是对柯西不等式的配凑.


科目:高中数学 来源: 题型:选择题
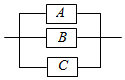 如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )
如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )| A. | 0.504 | B. | 0.994 | C. | 0.496 | D. | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{7π}{12}$ | |||
| Asin(ωx+φ) | 0 | 2 | -2 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
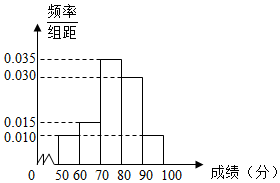 如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )
如图是100名学生某次数学测试成绩(单位:分)的频率分布直方图,则测试成绩在区间[50,70)中的学生人数是( )| A. | 30 | B. | 25 | C. | 22 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.
如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8+5$\sqrt{3}$ | B. | 4+5$\sqrt{3}$ | C. | 12 | D. | 4+5$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在α内必存在与a平行的直线,不一定存在与a垂直的直线 | |
| B. | 在α内不一定存在与a平行的直线,必存在与a垂直的直线 | |
| C. | 在α内必存在与a平行的直线.必存在与a垂直的直线 | |
| D. | 在α内不一定存在与a平行的直线.不-定存在与a垂直的直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com