
分析 (1)利用奇偶性的定义可得结论;
(2)根据函数单调性定义,可得函数f(x)在区间(0,2]上是减函数,在区间[2,+∞)上是增函数;
解答 解:(1)若x<0,则-x>0,则f(-x)=-x-$\frac{4}{x}$+1=f(x),
若x>0,则-x<0,则f(-x)=x+$\frac{4}{x}$+1=f(x),
综上f(-x)=f(x),即函数f(x)是偶函数.
(2)当x>0时,$f(x)=x+\frac{4}{x}+1$
设0<x1<x2,则$f({x_1})-f({x_2})=\frac{{({x_1}-{x_2})({x_1}{x_2}-4)}}{{{x_1}{x_2}}}$
∴当0<x1<x2≤2时,f(x1)-f(x2)>0即f(x1)>f(x2)
当2≤x1<x2时,f(x1)-f(x2)<0即f(x1)<f(x2).
∴函数f(x)在区间(0,2]上是减函数,在区间[2,+∞)上是增函数.
点评 本题考查函数的奇偶性与单调性,利用函数奇偶性和单调性的定义是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:解答题
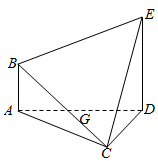 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O的半径OC垂直于直径AB,M为BO上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.
如图,⊙O的半径OC垂直于直径AB,M为BO上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
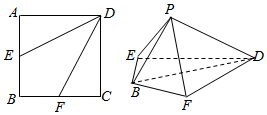 如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A | B | C | D | E |
| 总成绩(x) | 482 | 383 | 421 | 364 | 362 |
| 数学成绩(y) | 78 | 65 | 71 | 64 | 61 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com