
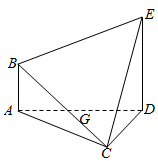
 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.分析 (1)根据线面平行的判定定理进行判断即可.
(2)根据二面角的定义,作出二面角的平面角,进行求解即可.
(3)根据三棱锥的体积公式进行求解即可.
解答 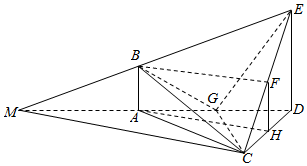 解:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
解:(1)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥=$\frac{1}{2}$ED,
∴FH∥=AB,∴四边形ABFH是平行四边形,
∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,
∴BF∥平面ACD;…(4分)
(2)将EB,DA分别延长相较于点M,连接MC
可证得△DCF,△ECF均为直角三角形,且DC⊥CF,EC⊥CF
∴∠ECD即为所求二面角的平面角
在Rt△CDE中,$CD=DE=2,CE=2\sqrt{2}$
∴∠ECD=45°
(3)连接BG、CG、EG,得三棱锥C-BGE,由ED⊥平面ACD,
∴平面ABED⊥平面ACD,又CG⊥AD,
∴CG⊥平面ABED,
则${V_{E-BGC}}={V_{C-BGE}}=\frac{1}{3}{S_{△BGE}}×GC=\frac{1}{3}×\frac{3}{2}×\sqrt{3}=\frac{{\sqrt{3}}}{2}$.
点评 本题主要考查线面平行,二面角的求解以及空间几何体的体积的计算,利用二面角平面角的定义以及三棱锥的体积公式进行转化是解决本题的关键.综合性较强.


科目:高中数学 来源: 题型:解答题
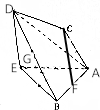 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC,BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC,BD,G为BD的中点,AB=AC=AE=BE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,且AE∥CD.
如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,且AE∥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | |
| 无意愿生二胎 | 20 | 25 | |
| 总计 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
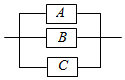 如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )
如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )| A. | 0.504 | B. | 0.994 | C. | 0.496 | D. | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
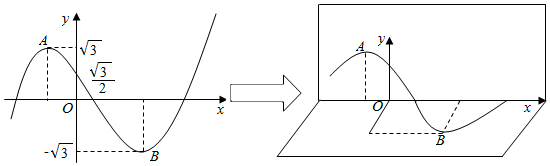
| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com