
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | |
| 无意愿生二胎 | 20 | 25 | |
| 总计 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
分析 (1)直接利用k2运算法则求解,判断生二胎意愿与性别是否有关的结论.
(2)利用独立重复试验真假求解所求的结果即可.
(3)求出X的可能值,求出概率,得到分布列,然后求解期望.
解答 解:(1)由于${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{90(25×30-15×20)^{2}}{50×40×45×45}$=4.5<6.635.
故没有99%以上的把握认为“生二胎意愿与性别有关”.
(2)由题意可得,一名男公务员要生二胎意愿的概率为$\frac{30}{30+20}$=$\frac{3}{5}$,无意愿的概率为$\frac{20}{30+20}$=$\frac{2}{5}$,
记事件A:这三人中至少有一人要生二胎,且各人意愿相互独立
则 P(A)=1-$P(\overline{A})$=1-$\frac{2}{5}×\frac{2}{5}×\frac{2}{5}$=$\frac{117}{125}$.
答:这三人中至少有一人有意愿生二胎的概率为:$\frac{117}{125}$.
(3)X可能的取值为0,1,2
P(X=0)=$\frac{{C}_{13}^{2}}{{C}_{15}^{2}}$=$\frac{26}{35}$;P(X=1)=$\frac{{C}_{2}^{1}{C}_{13}^{1}}{{C}_{15}^{2}}$=$\frac{26}{105}$;P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{15}^{2}}$=$\frac{1}{105}$.
| X | 0 | 1 | 2 |
| P | $\frac{26}{35}$ | $\frac{26}{105}$ | $\frac{1}{105}$ |
点评 本题考查独立检验,离散性随机变量的分布列,期望的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
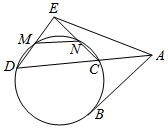 如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.
如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
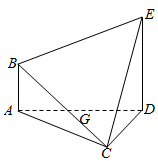 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2$\sqrt{3}$) | B. | $(2\sqrt{3},2)$ | C. | $(2\sqrt{2},2\sqrt{2})$ | D. | (-2$\sqrt{3}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com