
分析 (1)展开等式右边的二倍角正弦,约分后移项,利用两角和的正弦化简,再由已知结合正弦定理得答案;
(2)利用余弦定理求出cosC,再由平方关系求得sinC,代入面积公式求得△ABC的面积.
解答 解:(1)由2cos2AsinB=(2-cosB)sin2A,得
2cos2AsinB=2(2-cosB)sinAcosA,即sinAcosB+cosAsinB=2sinA,
∴sin(A+B)=2sinA,
∴sinC=2sinA,
又a=$\sqrt{6}$,
∴c=a•$\frac{sinC}{sinA}$=$\sqrt{6}×2=2\sqrt{6}$;
(2)∵a=$\sqrt{6}$,b=4,c=$2\sqrt{6}$,
∴$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{(\sqrt{6})^{2}+{4}^{2}-(2\sqrt{6})^{2}}{2×\sqrt{6}×4}$=$-\frac{\sqrt{6}}{24}$,
∴sinC=$\sqrt{1-(-\frac{\sqrt{6}}{24})^{2}}$=$\frac{\sqrt{570}}{24}$.
∴${S}_{△ABC}=\frac{1}{2}ab•sinC=\frac{1}{2}×\sqrt{6}×4×\frac{\sqrt{570}}{24}$=$\frac{\sqrt{95}}{2}$.
点评 本题考查同角三角函数的恒等变换应用,考查三角形的解法,训练了正弦定理和余弦定理在解三角形中的应用,是中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
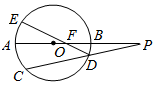 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F,且AB=2BP=8,
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F,且AB=2BP=8,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | |
| 无意愿生二胎 | 20 | 25 | |
| 总计 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | 与P的位置有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com