
分析 由题意求得变换矩阵T,根据二阶矩阵的求法,求得行列式丨A丨及其伴随矩阵,即可求得逆矩阵A-1.
解答 解:由题意可知设变换矩阵T=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,
∴$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{x+2y}\\{y}\end{array}]$,
∴$\left\{\begin{array}{l}{ax+by=x+2y}\\{cx+dy=y}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\\{c=0}\\{d=1}\end{array}\right.$,
∴A=$[\begin{array}{l}{1}&{2}\\{0}&{1}\end{array}]$,
丨A丨=1
∴逆矩阵A-1=$[\begin{array}{l}{1}&{-2}\\{0}&{1}\end{array}]$.
点评 本题考查矩阵的变换,考查逆变换与逆矩阵,矩阵变换是附加题中常考的,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
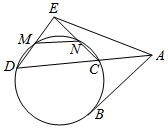 如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.
如图,已知AB,ACD分别为圆的一条切线和一条割线,M,N为圆上两点,DM延长线与CN延长线交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2$\sqrt{3}$) | B. | $(2\sqrt{3},2)$ | C. | $(2\sqrt{2},2\sqrt{2})$ | D. | (-2$\sqrt{3}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
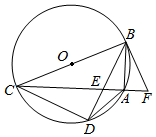 如图,四边形ABCD内接于⊙O,BC是⊙O的直径,A是$\widehat{BD}$的中点,AC交BD于点E,过⊙O上点B的切线与CA的延长线交于点F.
如图,四边形ABCD内接于⊙O,BC是⊙O的直径,A是$\widehat{BD}$的中点,AC交BD于点E,过⊙O上点B的切线与CA的延长线交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com