
分析 (1)由题意可得直线l的参数方程:$\left\{\begin{array}{l}{x=2+tcosα}\\{y=\frac{3}{2}+tsinα}\end{array}\right.$(t为参数).曲线C:(x-1)2+(y-2)2=1展开把y=ρsinθ,x=ρcosθ,ρ2=x2+y2代入即可化为极坐标方程.
(2)把直线l的参数方程:$\left\{\begin{array}{l}{x=2+tcosα}\\{y=\frac{3}{2}+tsinα}\end{array}\right.$(t为参数)代入曲线C的方程可得:t2+(2cosα-sinα)t+$\frac{1}{4}$=0,利用根与系数的关系代入$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{1}{|{t}_{1}|}+\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}+{t}_{2}|}{|{t}_{1}{t}_{2}|}$,即可得出.
解答 解:(1)由题意可得直线l的参数方程:$\left\{\begin{array}{l}{x=2+tcosα}\\{y=\frac{3}{2}+tsinα}\end{array}\right.$(t为参数).
曲线C:(x-1)2+(y-2)2=1展开可得:x2+y2-2x-4y+4=0,
把y=ρsinθ,x=ρcosθ,ρ2=x2+y2代入化为极坐标方程:ρ2-2ρcosθ-4ρsinθ+4=0.
(2)把直线l的参数方程:$\left\{\begin{array}{l}{x=2+tcosα}\\{y=\frac{3}{2}+tsinα}\end{array}\right.$(t为参数)代入曲线C的方程:x2+y2-2x-4y+4=0,
可得:t2+(2cosα-sinα)t+$\frac{1}{4}$=0,由△>0,可得|2cosα-sinα|>1.
故$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{1}{|{t}_{1}|}+\frac{1}{|{t}_{2}|}$=$\frac{|{t}_{1}+{t}_{2}|}{|{t}_{1}{t}_{2}|}$=4|2cosα-sinα|∈$(4,4\sqrt{5}]$.
点评 本题考查了直角坐标与极坐标的互化、三角函数基本关系式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,2017) | B. | (0,2018) | C. | (2017,+∞) | D. | (2018,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
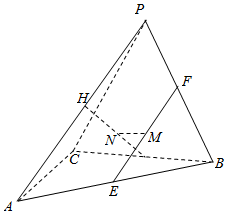 如图,在四面体PABC中,平面PBC⊥平面ABC,△ABC为等腰直角三角形,且∠C=90°,PB=PC,点E,F,G,H分别是线段AB,BP,BC,PA的中点,点M,N分别是EF,GH的中点.
如图,在四面体PABC中,平面PBC⊥平面ABC,△ABC为等腰直角三角形,且∠C=90°,PB=PC,点E,F,G,H分别是线段AB,BP,BC,PA的中点,点M,N分别是EF,GH的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直线ED与圆相切于点D,且平行于弦BC,连接EC并延长,交圆于点A,弦BC和AD相交于点F.
如图,直线ED与圆相切于点D,且平行于弦BC,连接EC并延长,交圆于点A,弦BC和AD相交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | 与P的位置有关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com