
分析 由B=[A丨I],对A与I进行完全相同的若干初等行变换,把A化为单位矩阵,将单位矩阵化为A-1.
解答 解:B=[A丨I]=$[\begin{array}{l}{1}&{0}&{1}&{0}&{1}&{0}&{0}&{0}\\{2}&{1}&{2}&{0}&{0}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}&{0}&{0}&{1}&{0}\\{1}&{1}&{1}&{1}&{0}&{0}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{1}&{0}&{1}&{0}&{0}&{0}\\{0}&{1}&{0}&{0}&{-2}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}&{0}&{0}&{1}&{0}\\{0}&{1}&{0}&{1}&{-1}&{0}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{1}&{0}&{1}&{0}&{0}&{0}\\{0}&{1}&{0}&{0}&{-2}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}&{0}&{0}&{1}&{0}\\{0}&{0}&{0}&{1}&{1}&{-1}&{0}&{1}\end{array}]$
→$[\begin{array}{l}{1}&{0}&{0}&{0}&{1}&{0}&{-1}&{0}\\{0}&{1}&{0}&{0}&{-2}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}&{0}&{0}&{1}&{0}\\{0}&{0}&{0}&{1}&{1}&{-1}&{0}&{1}\end{array}]$,
逆矩阵A-1=$[\begin{array}{l}{1}&{0}&{-1}&{0}\\{-2}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}\\{1}&{-1}&{0}&{1}\end{array}]$.
点评 本题考查矩阵初等行变换法求矩阵的逆矩阵,考查计算能力,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,CD是∠ACB的角平分线,△ACD的外接圆交BC于E点.
如图,在△ABC中,CD是∠ACB的角平分线,△ACD的外接圆交BC于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
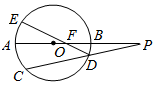 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F,且AB=2BP=8,
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F,且AB=2BP=8,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
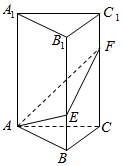 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com