
分析 (Ⅰ)由题意得$\left\{{\begin{array}{l}{1+{{(1-b)}^2}={r^2}}\\{\frac{1-b}{1-0}=1}\end{array}}\right.$,解出即可得出.
(Ⅱ)设Q(x,y),则$\overrightarrow{PQ}=(x-1,y-1),\overrightarrow{MQ}=(x+2,y+2)$,利用数量积运算性质及其圆的方程即可得出.$\overrightarrow{PQ}•\overrightarrow{MQ}$=x+y-2,记x+y=t,则y=-x+t,联立$\left\{{\begin{array}{l}{{x^2}+{y^2}=2}\\{y=-x+t}\end{array}}\right.$,得2x2-2tx+t2-2=0,利用△≥0,解出即可得出.
(Ⅲ)由过点P可以作两条不同直线AP,BP,且两条直线的倾斜角互补,可得两条直线的斜率存在且不为0.
设直线AP:y-1=k(x-1),则直线BP:y-1=-k(x-1),设点A(x1,y1),B(x2,y2),(x1≠x2).联立得(k2+1)x2-2k(k-1)x+k2-2k-1=0,利用根与系数的关系可得坐标,再利用斜率计算公式即可得出.
解答 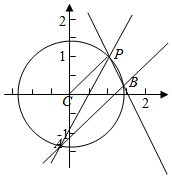 解:(Ⅰ)由题意得$\left\{{\begin{array}{l}{1+{{(1-b)}^2}={r^2}}\\{\frac{1-b}{1-0}=1}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{b=0}\\{{r^2}=2}\end{array}}\right.$,
解:(Ⅰ)由题意得$\left\{{\begin{array}{l}{1+{{(1-b)}^2}={r^2}}\\{\frac{1-b}{1-0}=1}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{b=0}\\{{r^2}=2}\end{array}}\right.$,
∴圆C的方程为x2+y2=2.
(Ⅱ)设Q(x,y),则$\overrightarrow{PQ}=(x-1,y-1),\overrightarrow{MQ}=(x+2,y+2)$,
∴$\overrightarrow{PQ}•\overrightarrow{MQ}$=(x-1)(x+2)+(y-1)(y+2)=x2+y2+x+y-4=x+y-2,
记x+y=t,则y=-x+t,由$\left\{{\begin{array}{l}{{x^2}+{y^2}=2}\\{y=-x+t}\end{array}}\right.$,得2x2-2tx+t2-2=0,
∵方程有实根,∴△=4t2-4×2×(t2-2)=4(4-t2)≥0,
解不等式得-2≤t≤2,∴当t=-2时,x+y取最小值-2,
∴$\overrightarrow{PQ}•\overrightarrow{MQ}$的最小值为-4.
(Ⅲ)∵过点P可以作两条不同直线AP,BP,且两条直线的倾斜角互补,∴两条直线的斜率存在且不为0.
设直线AP:y-1=k(x-1),则直线BP:y-1=-k(x-1),设点A(x1,y1),B(x2,y2),(x1≠x2).
由$\left\{{\begin{array}{l}{y-1=k(x-1)}\\{{x^2}+{y^2}=2}\end{array}}\right.$,得(k2+1)x2-2k(k-1)x+k2-2k-1=0,
方程的解是点A、P的横坐标,于是1+${x_1}=\frac{2k(k-1)}{{{k^2}+1}}$,则${x_1}=\frac{{{k^2}-2k-1}}{{{k^2}+1}}$;
同理得${x_2}=\frac{{{k^2}+2k-1}}{{{k^2}+1}}$,于是${x_1}+{x_2}=\frac{{2({k^2}-1)}}{{{k^2}+1}}$,${x_1}-{x_2}=\frac{-4k}{{{k^2}+1}}$.
∴直线AB的斜率$k=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{{[k({x_1}-1)+1]-[-k({x_2}-1)+1]}}{{{x_1}-{x_2}}}=\frac{{k({x_1}+{x_2})-2k}}{{{x_1}-{x_2}}}=1$,
又直线CP的斜率也为1,所以CP∥AB.
点评 本题考查了圆的方程及其性质、直线与圆的位置关系及其应用、数量积运算性质、一元二次方程的根与系数的关系、斜率与平行线之间的关系,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| P(k2≥k0) | 0.05 | 0.01 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | {0,1} | C. | (-1,$\sqrt{e}$] | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
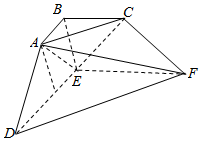 如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.
如图,三棱台ABC-DEF中,BE⊥底面DEF,AB=BE=$\frac{1}{2}$DE=1,∠ABC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com