
分析 先化简函数的解析式,结合解析式,利用函数的图象特征,作出函数的图象.
解答  解:(1)f(x)=-$\frac{1}{x+2}$=$\frac{-1}{x+2}$,它的图象关于点(-2,0)对称,
解:(1)f(x)=-$\frac{1}{x+2}$=$\frac{-1}{x+2}$,它的图象关于点(-2,0)对称,
相当于把y=$\frac{-1}{x}$的图象向左平移了2个单位得到的,如图(1)所示.
(2)f(x)=|x|•|x-2|=|x(x-2)|,先作出y=x(x-2)的图象,再把它的图象位于x轴上方的部分不变,
吧图象位于x轴下方的部分沿x轴对称到x轴上方,即可,如图(2)所示.
(3)f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤0}\\{-2x+2,x>0}\end{array}\right.$.的图象如图(3)所示.
点评 本题主要考查函数的图象特征,用变换法作函数的图象,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
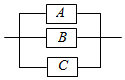 如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )
如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为( )| A. | 0.504 | B. | 0.994 | C. | 0.496 | D. | 0.06 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.
如图所示,PA为半径等于2的圆O的切线,A为切点,PO交圆O于B,C两点,$PA=\sqrt{5}$,∠BAC的角平分线与BC交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com