
分析 (1)在直角坐标系中,求出直线的方程,利用极坐标与直角坐标的互化公式求得直线极坐标方程.直接写出椭圆C的参数方程.
(2)设与x+y-2$\sqrt{2}$=0平行的直线方程为x+y+m=0,即y=-x-m与椭圆方程联立,利用判别式,即可得出结论.
解答 解:(1)在直角坐标系中,过点 M(2,$\frac{π}{4}$),且与极轴所成的角为$\frac{3π}{4}$的直线的斜率为-1,
其直角坐标方程是y-$\sqrt{2}$=-(x-$\sqrt{2}$),即x+y-2$\sqrt{2}$=0,
其极坐标方程为 ρcosθ+ρsinθ-2$\sqrt{2}$=0,
即ρcos(θ-$\frac{π}{4}$)=2.
椭圆C的参数方程$\left\{\begin{array}{l}{x=acosα}\\{y=sinα}\end{array}\right.$(α为参数);
(2)设与x+y-2$\sqrt{2}$=0平行的直线方程为x+y+m=0,即y=-x-m,
代入$\frac{{x}^{2}}{a^2}$+y2=1整理可得(1+a2)x2+2a2mx+m2a2-a2=0,
△=4a4m2-4(1+a2)(m2a2-a2)=0,∴m=±$\sqrt{1+{a}^{2}}$,x=-$\frac{2{a}^{2}}{1+{a}^{2}}$,y=$\sqrt{1+{a}^{2}}$+$\frac{2{a}^{2}}{1+{a}^{2}}$
∴点P到直线l的距离的最小值为$\frac{|\sqrt{1+{a}^{2}}-2\sqrt{2}|}{\sqrt{2}}$,对应点P的直角坐标(-$\frac{2{a}^{2}}{1+{a}^{2}}$,$\sqrt{1+{a}^{2}}$+$\frac{2{a}^{2}}{1+{a}^{2}}$).
点评 本题考查考查直线与椭圆的位置关系,考查极坐标方程与直角坐标方程的互化,求出直角坐标系中直线的方程是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是圆O的内接四边形,其中AB=AC,∠ABD=∠CBD,AC与BD交于点F,直线BC与AD交于点E.
如图,四边形ABCD是圆O的内接四边形,其中AB=AC,∠ABD=∠CBD,AC与BD交于点F,直线BC与AD交于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
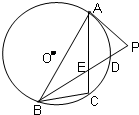 已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.
已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(k2≥k0) | 0.05 | 0.01 |
| k0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | {0,1} | C. | (-1,$\sqrt{e}$] | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com