
分析 (I)设点M的极坐标为M(ρ,θ),由题意可得:$\frac{ρ}{ρsinθ+p}$=e,可得曲线C的极坐标方程为:$ρ=\frac{ep}{1-esinθ}$,对e分类讨论即可得出.
(II)由e=1,p=1得:曲线C的极坐标方程为ρ-ρsinθ=1,化成直角坐标方程:x2=2y+1.直线l:ρ=$\frac{4}{cosθ-2sinθ}$,把y=ρsinθ,x=ρcosθ代入化为直角坐标方程.点M,N分别为曲线C和直线l上的动点,设M(x0,y0).|MN|的最小值就是M到l的距离最小值,利用点到直线的距离公式及其二次函数的单调性即可得出.
解答 解:(I)设点M的极坐标为M(ρ,θ),由题意可得:$\frac{ρ}{ρsinθ+p}$=e,
∴曲线C的极坐标方程为:$ρ=\frac{ep}{1-esinθ}$,
若0<e<1时,曲线C是椭圆;
若e=1时,曲线C是抛物线;
若e>1时,曲线C是双曲线.
(II)由e=1,p=1得:曲线C的极坐标方程为ρ-ρsinθ=1,可得ρ=y+1,两边平方可得:ρ2=x2+y2=y2+2y+1,
化成直角坐标方程:x2=2y+1.
直线l:ρ=$\frac{4}{cosθ-2sinθ}$的直角坐标方程为x-2y-4=0,
点M,N分别为曲线C和直线l上的动点,设M(x0,y0).
|MN|的最小值就是M到l的距离最小值,
∴|MN|min=$\frac{|{x}_{0}-2{y}_{0}-4|}{\sqrt{5}}$=$\frac{|{x}_{0}^{2}-{x}_{0}+3|}{\sqrt{5}}$=$\frac{({x}_{0}-\frac{1}{2})^{2}+\frac{11}{4}}{\sqrt{5}}$$≥\frac{11\sqrt{5}}{20}$,
当${x}_{0}=\frac{1}{2}$时,取“=”.
∴|MN|的最小值为$\frac{11\sqrt{5}}{20}$,此时M点的坐标为M$(\frac{1}{2},-\frac{3}{8})$.
点评 本题考查了直角坐标与极坐标的互化、点到直线的距离公式、二次函数的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
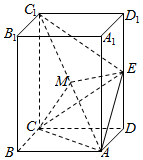 如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.
如图所示,正四棱柱ABCD-A1B1C1D1的底面边长为1,DD1=2,E为DD1的中点,连结C1E,CE,AC,AE,AC1,B1E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:已知⊙O是△ABC的外接圆,AB=BC,AH是BC边上的高,延长交⊙O于点D,AE是⊙O的直径.
如图:已知⊙O是△ABC的外接圆,AB=BC,AH是BC边上的高,延长交⊙O于点D,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com