
���� ��1����ԲC�ļ����귽��Ϊ��=4sin�ȣ��Ӽ�����ԲC���ң���������е�M���ѣ��ȣ�����2�ѣ��ȣ���ԲC�ϣ����뼴��C1�ļ����귽�̣�
��2������l�IJ�������Ϊ$\left\{\begin{array}{l}{x=tcos��}\\{y=tsin��}\end{array}\right.$����0�ܦ����У�tΪ��������t��0������Ϊy=xtan����������ɵã�|OA|=��1=4sin����|OB|=��2=2sin��������|$\overrightarrow{AB}$|=$\sqrt{3}$�����ɵó���
��� �⣺��1����ԲC�ļ����귽��Ϊ��=4sin�ȣ�
�Ӽ�����ԲC���ң���������е�M���ѣ��ȣ���
��2�ѣ��ȣ���ԲC�ϣ�
��C1�ļ����귽��Ϊ2��=4sin�ȣ�
�ɵæ�=2sin�ȣ�
��2������l�IJ�������Ϊ$\left\{\begin{array}{l}{x=tcos��}\\{y=tsin��}\end{array}\right.$����0�ܦ����У�tΪ��������t��0������Ϊy=xtan����
������ɵã�|OA|=��1=4sin����|OB|=��2=2sin����
��|$\overrightarrow{AB}$|=$\sqrt{3}$��
��|OA|-|OB|=2sin��=$\sqrt{3}$����sin��=$\frac{\sqrt{3}}{2}$��
��0�ܦ����У�
��$��=\frac{��}{3}$�����=$\frac{2��}{3}$��
���� ���⿼����ֱ�������뼫����Ļ������������̻�Ϊ��ͨ���̡�����֮��ľ��롢Բ�����ʣ�������������������������������е��⣮


 ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
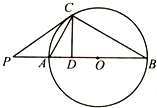 ��ͼ��PΪ��O���һ�㣬ֱ��PO���O��A��B���㣬CΪ��O��һ�㣬CD��PO��PO��D��CAƽ�֡�PCD��
��ͼ��PΪ��O���һ�㣬ֱ��PO���O��A��B���㣬CΪ��O��һ�㣬CD��PO��PO��D��CAƽ�֡�PCD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
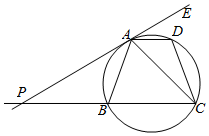 ��֪����ͼԲO��������AD��BC����AΪ�е�����߽�CB�ӳ�����P����֤��
��֪����ͼԲO��������AD��BC����AΪ�е�����߽�CB�ӳ�����P����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com