
分析 (1)由已知利用平面向量的坐标运算可得$\overrightarrow{b}+\overrightarrow{c}$=(sinx-2cosx,sinx),利用三角函数恒等变换的应用可得|$\overrightarrow{b}+\overrightarrow{c}$|2=$\sqrt{5}$cos(2x+φ)+3,其中,tanφ=2,又x∈[0,$\frac{π}{4}$],可求$2x+φ∈[φ,\frac{π}{2}+φ]$,利用余弦函数的单调性即可得解|$\overrightarrow{b}$+$\overrightarrow{c}$|的取值范围;
(2)利用平面向量数量积的运算可得g(x)=-3sinxcosx+k(sinx-cosx)-k2,令t=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),则g(x)可化为$h(t)=(-3)•\frac{{1-{t^2}}}{2}+kt-{t^2}=\frac{3}{2}{t^2}+kt-{k^2}-\frac{3}{2},t∈[{-\sqrt{2},\sqrt{2}}]$,对称轴$t=-\frac{k}{{2×\frac{3}{2}}}=-\frac{k}{3}$.利用二次函数的图象和性质分类讨论即可得解.
解答 解:(1)$\overrightarrow{b}+\overrightarrow{c}$=(sinx-2cosx,sinx),
|$\overrightarrow{b}+\overrightarrow{c}$|2=(sinx-2cosx,sinx)2
=2sin2x-4sinxcosx+4cos2x
=2cos2x-4sinxcosx+2
=cos2x-2sin2x+3
=$\sqrt{5}$cos(2x+φ)+3,其中,tanφ=2,
又∵x∈[0,$\frac{π}{4}$],
∴$2x+φ∈[φ,\frac{π}{2}+φ]$,
∴$\sqrt{5}cos(2x+φ)$在$[φ,\frac{π}{2}+φ]$上单调递减,
∴|$\sqrt{5}$cos(2x+φ)|2∈[1,4],
∴|$\overrightarrow{b}$+$\overrightarrow{c}$|∈[1,2].
(2)$\overrightarrow{a}+\overrightarrow{b}$=(2sinx,cosx+k),
g(x)=($\overrightarrow{a}+\overrightarrow{b}$)$•\overrightarrow{c}$
=-4sinxcosx+(cosx+k)(sinx-k)
=-3sinxcosx+k(sinx-cosx)-k2
令t=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$),
则t∈[-$\sqrt{2}$,$\sqrt{2}$],且t2=sin2x+cos2x-2sinxcosx=1-2sinxcosx,
所以$sinxcosx=\frac{{1-{t^2}}}{2}$.
所以g(x)可化为$h(t)=(-3)•\frac{{1-{t^2}}}{2}+kt-{t^2}=\frac{3}{2}{t^2}+kt-{k^2}-\frac{3}{2},t∈[{-\sqrt{2},\sqrt{2}}]$,
对称轴$t=-\frac{k}{{2×\frac{3}{2}}}=-\frac{k}{3}$.
①当$-\frac{k}{3}<-\sqrt{2}$,即$k>3\sqrt{2}$时,$g{(x)_{min}}=h(-\sqrt{2})=\frac{3}{2}×{(-\sqrt{2})^2}+k(-\sqrt{2})-{k^2}-\frac{3}{2}=-{k^2}-\sqrt{2}k+\frac{3}{2}$,
由$-{k^2}-\sqrt{2}k+\frac{3}{2}=-\frac{3}{2}$,得${k^2}+\sqrt{2}k-3=0$,
所以$k=\frac{{-\sqrt{2}±\sqrt{14}}}{2}$.
因为$k>3\sqrt{2}$,
所以此时无解.
②当$-\sqrt{2}≤-\frac{k}{3}≤\sqrt{2}$,即$-3\sqrt{2}≤k≤3\sqrt{2}$时,$g{(x)_{min}}=h(-\frac{k}{3})=\frac{3}{2}{(-\frac{k}{3})^2}+k(-\frac{k}{3})-{k^2}-\frac{3}{2}=-\frac{7}{6}{k^2}-\frac{3}{2}$.
由-$\frac{7{k}^{2}}{6}$-$\frac{3}{2}$=-$\frac{3}{2}$,得k=0∈[-3$\sqrt{2}$,3$\sqrt{2}$].
③当-$\frac{k}{3}$$>\sqrt{2}$,即k<-3$\sqrt{2}$时,
g(x)min=h($\sqrt{2}$)=-k2+$\sqrt{2}$k+$\frac{3}{2}$,
由-k2+$\sqrt{2}$k+$\frac{3}{2}$=-$\frac{3}{2}$,得k2-$\sqrt{2}$k-3=0,
所以k=$\frac{\sqrt{2}±\sqrt{14}}{2}$.
因为k$<-3\sqrt{2}$,所以此时无解.
综上所述,当k=0时,g(x)的最小值为-$\frac{3}{2}$.
点评 本题主要考查了三角函数中的恒等变换应用,平面向量的坐标运算,平面向量数量积的运算,考查了计算能力和分类讨论思想,属于中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
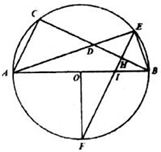 如图,AB是圆O的直径,点D是弦BC的中点,直线AD交圆O于点E,过点E作EF⊥BC于点H,交圆O于点F,交AB于点I,若OF⊥AB.
如图,AB是圆O的直径,点D是弦BC的中点,直线AD交圆O于点E,过点E作EF⊥BC于点H,交圆O于点F,交AB于点I,若OF⊥AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com