
分析 讨论当x>0,和x<0时,函数g(x)=x2-ax+2a的取值情况,利用参数分离法进行求解即可.
解答 解:函数的定义域为(-1,+∞),设g(x)=x2-ax+2a,
若-1<x<0,ln(x+1)<0,此时要求g(x)在-1<x<0经过二、三,
即此时$\left\{\begin{array}{l}{g(0)=2a<0}\\{g(-1)=1+a+2a>0}\end{array}\right.$,即$\left\{\begin{array}{l}{a<0}\\{a>-\frac{1}{3}}\end{array}\right.$,此时-$\frac{1}{3}$<a<0,
当x=0时,f(0)=0,此时函数图象过原点,
当x>0时,ln(x+1)>0,此时要求g(x)经过一四象限,
即x>0时,x2-ax+2a<0,有解,
即a(x-2)<x2有解,
当x=2时,不等式等价为0<4,成立,
当0<x<2时,a>$\frac{{x}^{2}}{x-2}$,∵此时$\frac{{x}^{2}}{x-2}$<0,∴此时a<0,
当x>2时,不等式等价为a<$\frac{{x}^{2}}{x-2}$,
∵$\frac{{x}^{2}}{x-2}$=$\frac{(x-2)^{2}+4(x-2)+4}{x-2}$=(x-2)+$\frac{4}{x-2}$+4
≥4+2$\sqrt{(x-2)•\frac{4}{x-2}}$=4+2×2=4+4=8,
∴若a<$\frac{{x}^{2}}{x-2}$有解,则a>8,
即当x>0时,a<0或a>8,
综上{a|-$\frac{1}{3}$<a<0}∩{a|a<0或a>8}={a|-$\frac{1}{3}$<a<0}=(-$\frac{1}{3}$,0),
故答案为:(-$\frac{1}{3}$,0).
点评 本题主要考查函数图象的应用,根据条件当x>0和x<0时,ln(x+1)的符号一定,此时讨论g(x)=x2-ax+2a的符号,结合一元二次函数的图象和性质是解决本题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
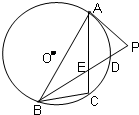 已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.
已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
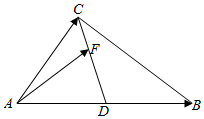 如图所示,在△ABC中,AD=DB,F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,$\overrightarrow{AF}$=$x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为$6+4\sqrt{2}$.
如图所示,在△ABC中,AD=DB,F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,$\overrightarrow{AF}$=$x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为$6+4\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com