
分析 点A的极坐标是(1,π),化为直角坐标A(-1,0).曲线C:ρ=2sinθ,即ρ2=2ρsinθ,把y=ρsinθ,ρ2=x2+y2代入即可化为直角坐标方程.可得圆心C,半径r.即可得出|PA|的取值范围是[|CA|-r,|CA|+r].
解答 解:点A的极坐标是(1,π),化为直角坐标A(-1,0).
曲线C:ρ=2sinθ,即ρ2=2ρsinθ,化为直角坐标方程:x2+y2=2y,配方为:x2+(y-1)2=1.可得圆心C(0,1),半径r=1.
则|CA|=$\sqrt{2}$.
则|PA|的取值范围是$[\sqrt{2}-1,\sqrt{2}+1]$.
故答案为:$[\sqrt{2}-1,\sqrt{2}+1]$.
点评 本题考查了直角坐标与极坐标的互化、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
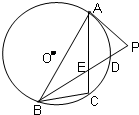 已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.
已知A,B,C,D为圆O上的四点,过A作圆O的切线交BD的延长线于点P,且PA=PE,∠ABC=45°,PD=1,BD=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com