
分析 通过对a取不同的值,求出A,结合集合的包含关系,求出a的范围即可.
解答 解:∵函数f(x)=|x+a|+|x-2|,
设h(x)=f(x)-|x-4|=|x+a|+|x-2|-|x-4|,
①当a=0时,h(x)=|x|+|x-2|-|x-4|,
h(-2)=2+4-6=0,
h(0)=0+2-4=-2,
h(2)=2+0-2=0,
h(4)=4+2-0=6,
∴函数h(x)图象由点A(-2,0),B(0,-2),C(2,0),D(4,6)连接起来,
可见h(x)≤0的解集为-2≤x≤2,包含[1,2],
②将A右移3个单位,
即a=-3时,h(x)=|x-3|+|x-2|-|x-4|,
h(1)=2+1-3=0,
h(2)=1+0-2=-1,
h(3)=0+1-1=0,
h(4)=1+2-0=3,
∴A(1,0),B(2,-1),C(3,0),D(4,3),
h(x)≤0的解集为1≤x≤3,包含[1,2],
∴-3≤a≤0,
故答案为:[-3,0].
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及集合的包含关系,是一道中档题.


科目:高中数学 来源: 题型:解答题
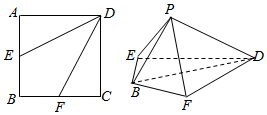 如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
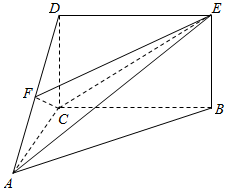 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=$\frac{1}{2}$BC=2,F是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或2 | B. | 2 | C. | 1或0 | D. | 0或1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A | B | C | D | E |
| 总成绩(x) | 482 | 383 | 421 | 364 | 362 |
| 数学成绩(y) | 78 | 65 | 71 | 64 | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com