练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知点P（2，-1）、Q（a，4），并且|PQ|=$\sqrt{41}$，求a的值．

    分析 根据题意，由P、Q的坐标以及|PQ|的值可得|PQ|=$\sqrt{（2-a）^{2}+（4+1）^{2}}$=$\sqrt{41}$，将其变形可得（a-2）2=16，解可得a的值，即可得答案．

    解答 解：根据题意，点P（2，-1）、Q（a，4），
    则|PQ|=$\sqrt{（2-a）^{2}+（4+1）^{2}}$=$\sqrt{41}$，
    即（a-2）2=16，
    解可得a=6或-2，
    故a的值为6或-2．

    点评 本题考查两点间距离公式的运用，解题的关键是正确利用两点间距离公式得到关于a的方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

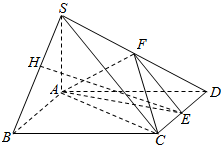    7．如图所示，已知四棱锥S-ABCD，底面ABCD为菱形，∠ABC=60°，SA⊥平面ABCD，E，F分别是CD，SD的中点，点H为SB上的动点，且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$．
    （1）证明：AE⊥SB；
    （2）求二面角E-AF-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．从装有2只红球、2只白球和1只黑球的袋中逐一取球，每只球被抽取的可能性相同．
    （1）若抽取后又放回，抽3次，分别求恰好2次为红球的概率及抽全三种颜色球的概率；
    （2）若抽取后不放回，求抽完红球所需次数不少于4次的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

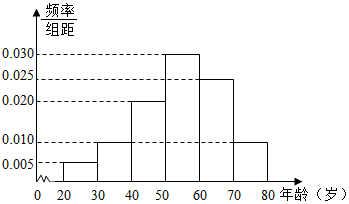    5．广场舞是现代城市群众文化、娱乐发展的产物，其兼具文化性和社会性，是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查，随机抽取了40名广场舞者进行调查，将他们年龄分成6段：[20，30），[30，40），[40，50），[50，60），[60，70），[70，80]后得到如图所示的频率分布直方图．
    （1）估计在40名广场舞者中年龄分布在[40，70）的人数；
    （2）求40名广场舞者年龄的中位数和平均数的估计值；
    （3）若从年龄在[20，40）中的广场舞者中任取2名，求这两名广场舞者年龄在[30，40）中的人数X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．2015年12月27日全国人大常委会会议通过了关于修教口与计划生育法的决定，“全面二孩”从2016年元旦起开给实施．A市妇联为了解该市市民对“全面二孩”政策的态度，随机抽取了男性市民45人、女性市民55人进行调查，得到以下2×2列联表．
      支持反对 合计 
    男性 30 15 45
     女性 45 10 55
     合计 75 25 100
    （1）根据以上数据，能否有90%的把握认为A市市民“支持全面二孩”与“性别”有关？
    （2）现从参与调查的女性用户中按分层抽样的方法选出11名发放礼品，在所抽取的11人中分别求出“支持”和“不支持”态度的人数；
    （3）将上述调查所得到的频率视为概率，现在从A市所有市民中，采取随机抽样的方法抽取3位市民进行长期跟踪调查，记被抽取的3位市民中持“支持”态度人数为X．
    ①求X的分布列；
    ②求X的数学期望E（X）和方差D（X）．
    附表及公式：
     P（K2≥k0） 0.150.10 0.05 0.025 0.010 
     k0 2.0722.7063.841 5.024 6.635 
    K2=$\frac{n（ad-bc）^2}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知A，B是锐角△ABC的两个内角，二次函数f（x）=m2x2-2m2x+1，那么（　　）
    A．f（sinA）＞f（cosA）B．f（cosA）＞f（sinA）C．f（cosA）＞f（sinB）D．f（sinA）＞f（cosB）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{x}，x≥0}\\{3x+1，x＜0}\end{array}\right.$，则不等式f（x）＜4f（x）+1的解集是{x|x＞-$\frac{1}{9}$}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知向量$\overrightarrow{m}$=（cosωx，a），$\overrightarrow{n}$=（a，2+$\sqrt{3}$sinωx），ω＞0，函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-5（a∈R，a≠0）．
    （1）当函数f（x）在x∈R上的最大值为3时，求a的值；
    （2）在（1）的条件下，若函数y=f（x）-1在x∈（0，π]上至少有5个零点，求ω的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数y=acos（2x+$\frac{π}{3}$）+3，x∈R的最大值为4，求实数a的值．

    查看答案和解析>>

    同步练习册答案