
分析 (1)抽取后又放回,每次取球可看作独立重复试验,利用独立重复试验求解即可.
(2)抽取后不放回,分别求出4,5的概率,再求其和即可.
解答 解:(1)抽取一次取到红球的概率为$\frac{2}{5}$,
∴抽取3次恰好有两次取到红球的概率为C32($\frac{2}{5}$)2×($\frac{3}{5}$)=$\frac{36}{125}$,
抽全三种颜色的概率$\frac{2}{5}×\frac{2}{5}×\frac{1}{5}$×A33=$\frac{24}{125}$;
(2)抽取后不放回,抽完红球所需次数不少于4次,则为4次和5次
则其概率为$\frac{{C}_{2}^{1}{C}_{3}^{2}{A}_{3}^{3}}{{A}_{5}^{4}}$+$\frac{{C}_{2}^{1}{C}_{3}^{3}{A}_{4}^{4}}{{A}_{5}^{5}}$=$\frac{3}{10}$+$\frac{4}{10}$=$\frac{7}{10}$
点评 本题考查了概率公式问题,解题时要认真审题,仔细解答,注意排列组合和概率知识的灵活运用解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4或-3 | C. | -3或-1 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
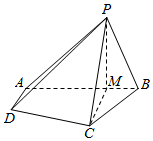 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com