
| A. | 4 | B. | 4或-3 | C. | -3或-1 | D. | -3 |
分析 求出原函数的导函数,设出A,B点的坐标,得到函数在A,B点处的导数值,由A,B点处的导数值相等得到3x12-2px1+3=3x22-2px2+3=m,把x1,x2看作方程3x2-2px+3-m=0的两个根,利用根与系数关系得到x1+x2=$\frac{2}{3}$p,进一步得到AB的中点坐标,然后再证明AB的中点在曲线C上,最后由AB中点的纵坐标相等求得实数p的值,注意检验.
解答 解:由y=x3-px2+3x,得y′=3x2-2px+3,
设A(x1,y1),B(x2,y2),
则曲线C在A,B处的切线的斜率分别为3x12-2px1+3,
3x22-2px2+3,
∵曲线C在A,B处的切线平行,
∴3x12-2px1+3=3x22-2px2+3,
令3x12-2px1+3=3x22-2px2+3=m,
∴x1,x2是方程3x2-2px+3-m=0的两个根,
则x1+x2=$\frac{2}{3}$p,
下面证线段AB的中点在曲线C上,
∵$\frac{{{x}_{1}}^{3}-p{{x}_{1}}^{2}+3{x}_{1}+{{x}_{2}}^{3}-p{{x}_{2}}^{2}+3{x}_{2}}{2}$
=$\frac{({x}_{1}+{x}_{2})[({x}_{1}+{x}_{2})^{2}-3{x}_{1}{x}_{2}]-p[({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}]+3({x}_{1}+{x}_{2})}{2}$
=$\frac{2p-\frac{4}{27}{p}^{3}}{2}$=p-$\frac{2}{27}$p3,
而($\frac{{x}_{1}+{x}_{2}}{2}$)3-p($\frac{{x}_{1}+{x}_{2}}{2}$)2+3•$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{1}{27}$p3-$\frac{1}{9}$p3+p
=p-$\frac{2}{27}$p3,
∴线段AB的中点在曲线C上,
由x1+x2=$\frac{2}{3}$p,知线段的中点为($\frac{1}{3}$p,$\frac{1}{9}$($\frac{1}{3}$p-8)),
∴-$\frac{8}{9}$+$\frac{1}{27}$p=p-$\frac{2}{27}$p3,解得p=-1,-3或4.
当p=-1时,y=x3+x2+3x的导数为y′=3x2+2x+3>0恒成立,
即函数为递增函数,直线与曲线只有一个交点,舍去;
p=-3,或4时,y=x3+3x2+3x单调,不成立.
p=4时,y=x3-px2+3x不单调,成立.
故选:A.
点评 本题考查利用导数研究曲线上某点的切线方程,求解该题的关键是利用AB中点的坐标相等,关键是证明AB的中点在曲线C上,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
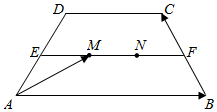 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 30 | 15 | 45 |
| 女性 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com