
分析 (I)根据正弦定理将边化角,化简得出cosC;
(II)根据三角形的面积公式列方程解出CD.
解答 解:(Ⅰ)∵acosB+bcosA=2ccosC,
∴sinAcosB+sinBcosA=2sinCcosC,
即sinC=2sinCcosC,
因为0<C<π,所以$cosC=\frac{1}{2}$,故$C=\frac{π}{3}$;
(Ⅱ)在△ABC中,∵CD平分∠ACB,∴$∠ACD=∠BCD=\frac{π}{6}$.
∵S△ABC=S△ACD+S△BCD,
∴2$\sqrt{3}$=$\frac{1}{2}$a$•CD•sin\frac{π}{6}$+$\frac{1}{2}•b•CD•sin\frac{π}{6}$=$\frac{1}{2}$(a+b)•CD•sin$\frac{π}{6}$.
解得$CD=\frac{{4\sqrt{3}}}{3}$.
点评 本题考查了正弦定理在解三角形中的应用,属于中档题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既不充分也不要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 充分必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
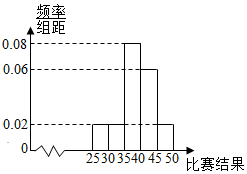 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4或-3 | C. | -3或-1 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com