
分析 (1)求函数的导数,利用导数的几何意义进行求解即可.
(2)构造函数G(x)=f(x)-g(x),将条件转化为G(x)<0,恒成立,求函数的导数,利用导数研究函数的最值问题即可得到结论.
解答 解:(1)函数f(x)的定义域为(0,+∞);
则f(1)=ln1+1=1,
f′(x)=1+$\frac{1}{x}$,
则f′(1)=1+1=2,
则曲线y=f(x)在点(1,f(1))处的切线方程为y-1=2(x-1),即y=2x-1;
(2)令G(x)=f(x)-g(x)=lnx-$\frac{1}{2}$mx2+(1-m)x+1,x>0,
若函数y=f(x)的图象始终在函数y=g(x)图象的下方,
等价为G(x)<0,恒成立,
即G(x)max<0恒成立,
G′(x)=$\frac{1}{x}$-mx+1-m=$\frac{-m{x}^{2}+(1-m)x+1}{x}$,(x>0),
①当m≤0时,∵x>0,∴G′(x)>0,
则G(x)在(0,+∞)上单调递增,∵G(1)=-$\frac{3}{2}$m+2>0,
∴f(x)的图象不可能在g(x)的图象的下方,
②当m>0时,G′(x)=$\frac{-m{x}^{2}+(1-m)x+1}{x}$=$\frac{-m(x-\frac{1}{m})(x+1)}{x}$,(x>0),
令G′(x)=0,得x=$\frac{1}{m}$,
当0<x<$\frac{1}{m}$时,G′(x)>0,函数G(x)递增,
当x>$\frac{1}{m}$时,G′(x)<0.函数G(x)递减,
即当x=$\frac{1}{m}$时,函数G(x)取得最大值G($\frac{1}{m}$)=ln$\frac{1}{x}$-$\frac{1}{2}$m•($\frac{1}{m}$)2+(1-m)•$\frac{1}{m}$+1=$\frac{1}{2m}$-lnm,
令r(m)=$\frac{1}{2m}$-lnm则r(m)在(0,+∞)上为减函数,
∵r(1)=$\frac{1}{2}$-ln1=$\frac{1}{2}>0$,r(2)=$\frac{1}{4}$-ln2<$\frac{1}{4}$-ln$\sqrt{e}$=-$\frac{1}{4}$<0,
∴当m≥2,r(m)<0,则m的最小值是2.
点评 本题主要考查导数的应用,求函数的导数根据导数的几何意义以及构造函数转换为最值恒成立问题是解决本题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≠0,c=0 | B. | a=0,c=0 | C. | c=0 | D. | c≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 逻辑思维能力 语言表达能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | m |
| 良好 | 4 | 4 | 1 |
| 优秀 | 1 | m | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 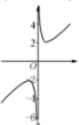 | B. | 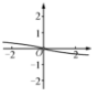 | C. |  | D. | 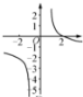 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
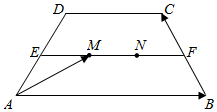 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com