
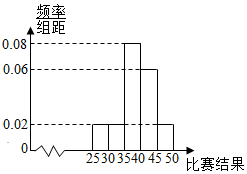
 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
分析 (1)由频率=$\frac{频数}{总数}$,利用频率分布直方图能求出a,b的值.
(2)根据频率分布直方图,能估计该项比赛结果的中位数.
(3)第1,2,3组共有300人,利用分层抽样在300名学生中抽取6名学生,第1组抽取的人数为1人,第2组抽取的人数为1人,第3组抽取的人数为4人,由此能求至少有1人比赛结果在第3组的概率.
解答 (本小题满分12分)
解:(1)由题设可知,a=0.08×5×500=200,b=0.02×5×500=50. …(3分)
(2)根据频率分布直方图,估计该项比赛结果的中位数为:35+$\frac{0.3}{0.08}$=38.75. …(6分)
(3)∵第1,2,3组共有50+50+200=300人,
∴利用分层抽样在300名学生中抽取6名学生,第1组抽取的人数为$\frac{6×50}{300}$=1,
第2组抽取的人数为$\frac{6×50}{300}$=1,第3组抽取的人数为$\frac{6×200}{300}$=4.…(8分)
记第1组抽取的1位同学为A,第2组抽取的1位同学为B,
第3组抽取的4位同学为C1,C2,C3,C4.
∴从6位同学中抽两位同学有:(A,B),(A,C1),(A,C2),(A,C3),(A,C4),(B,C1),
(B,C2),(B,C3),(B,C4),(C1,C2),(C1,C3),(C1,C4),(C2,C3),(C2,C4),(C3,C4).共有15种等可能. …(10分)
其中2人比赛结果都不在第3组的有:(A,B),共1种可能.
∴至少有1人比赛结果在第3组的概率为1-$\frac{1}{15}$=$\frac{14}{15}$. …(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 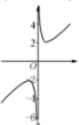 | B. | 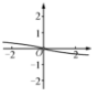 | C. |  | D. | 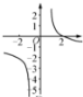 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
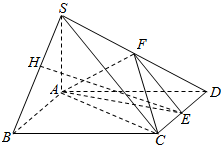 如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 30 | 15 | 45 |
| 女性 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com