
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先化简函数f(x)①根据函数的对称性进行判断,
②根据函数单调性进行判断,
③根据三角函数平移关系进行判断.
解答 解:函数$f(x)=2sinxcosx-2\sqrt{3}{cos^2}x+\sqrt{3}$=sin2x-$\sqrt{3}$(2cos2x-1)=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$),
①当$x=\frac{11π}{12}$时,2x-$\frac{π}{3}$=2×$\frac{11π}{12}$-$\frac{π}{3}$=$\frac{11π}{6}$-$\frac{π}{3}$=$\frac{9π}{6}$=$\frac{3π}{2}$,
则sin$\frac{3π}{2}$=-1,是最小值,故图象C关于直线$x=\frac{11π}{12}$对称正确,故①正确;
②当x∈$(-\frac{π}{12},\frac{5π}{12})$时,2x∈(-$\frac{π}{6}$,$\frac{5π}{6}$),2x-$\frac{π}{3}$∈(-$\frac{π}{2}$,$\frac{π}{2}$),此时函数f(x)是增函数;故②正确,
③由y=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到y=2sin2(x-$\frac{π}{3}$)=2sin(2x-$\frac{2π}{3}$),故不可以得到图象C;故③错误,
故正确的是①②,
故选:C.
点评 本题主要考查命题的真假判断,涉及三角函数的图象和性质,根据三角函数的倍角公式将函数进行化简是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$钱 | B. | $\frac{4}{3}$钱 | C. | $\frac{3}{2}$钱 | D. | $\frac{5}{3}$钱 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2] | B. | (-2,1] | C. | (0,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
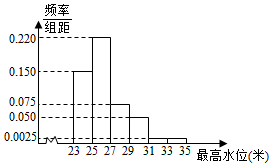 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
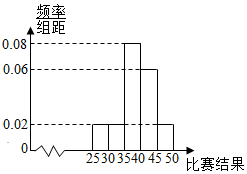 为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:
为了解我市高三学生参加体育活动的情况,市直属某校高三学生500人参加“体育基本素质技能”比赛活动,按某项比赛结果所在区间分组:第1组:[25,300,第2组:[30,35),第3组:[35,40),第4组:[40,45),第5组:[45,50],得到不完整的人数统计表如下:| 年龄所在区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
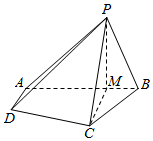 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com