
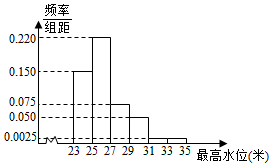
 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:分析 (Ⅰ)由题设得在未来3年里,河流最高水位X∈[27,31)发生的年数为Y,则Y~N(3,$\frac{1}{4}$),由此能求出未来3年里,至多有1年河流水位X∈[27,31)的概率.
(Ⅱ)由题设得P(23≤X<27)=0.74,P(31≤X≤35)=0.01,用X1,X2,X3分别表示方案一、方案二、方案三的损失,分别求出X1,X2,X3的数学期望,由此能求出结果.
解答 解:(Ⅰ)由题设得P(27≤X《31)=0.25=$\frac{1}{4}$,
∴在未来3年里,河流最高水位X∈[27,31)发生的年数为Y,则Y~N(3,$\frac{1}{4}$),
记事件“在未来3年里,至多有1年河流水位X∈[27,31)”为事件A,
则P(A)=P(Y=0)+P(Y=1)=${C}_{3}^{0}(\frac{3}{4})^{3}+{C}_{3}^{1}(\frac{3}{4})^{2}×\frac{1}{4}$=$\frac{27}{32}$,
∴未来3年里,至多有1年河流水位X∈[27,31)的概率为$\frac{27}{32}$.
(Ⅱ)由题设得P(23≤X<27)=0.74,
P(31≤X≤35)=0.01,
用X1,X2,X3分别表示方案一、方案二、方案三的损失,
由题意得X1=3800,
X2的分布列为:
| X2 | 2000 | 52000 |
| P | 0.99 | 0.01 |
| X3 | 0 | 10000 | 60000 |
| P | 0.74 | 0.25 | 0.01 |
点评 本题考查概率的求法,考查最佳方案的判断与求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:解答题
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
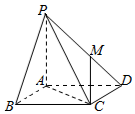 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=AB,点M在棱PD上,PB∥平面ACM.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
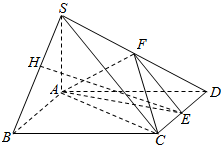 如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图所示,已知四棱锥S-ABCD,底面ABCD为菱形,∠ABC=60°,SA⊥平面ABCD,E,F分别是CD,SD的中点,点H为SB上的动点,且EH与平面SAB所成最大角的正切值为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{3}$ | C. | 1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
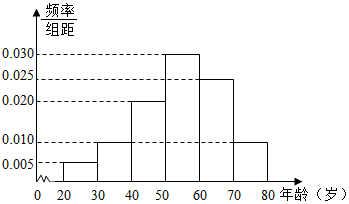 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com