
| A. | 4 | B. | $\sqrt{3}$ | C. | 1 | D. | -2 |
分析 求出ω,φ得到g(x)的解析式,根据余弦函数的图象和x的范围得出g(x)的最值.
解答 解:∵f(0)=$\frac{1}{2}$,∴sinφ=$\frac{1}{2}$,∴φ=$\frac{π}{6}$.
∵f(x)=-f(x+$\frac{π}{2}$),∴$sin(ωx+\frac{π}{6})=-sin[ω(x+\frac{π}{2})+\frac{π}{6}]$
∴$\frac{ωπ}{2}=π$,即ω=2.
∴$g(x)=2cos(2x+\frac{π}{6})$,
∵x∈[0,$\frac{π}{2}$],∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$
∴当2x+$\frac{π}{6}$=$\frac{π}{6}$时,g(x)取得最大值,${g_{max}}(x)=2cos\frac{π}{6}=\sqrt{3}$.
故选:B.
点评 本题考查了正余弦函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:解答题
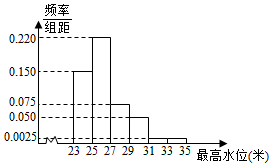 根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:
根据某水文观测点的历史统计数据,得到某河流每年最高水位X(单位:米)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com