
分析 根据条件可得到f(0)=0,从而由log2x•f(x)>0可得到$\left\{\begin{array}{l}{lo{g}_{2}x>0}\\{f(x)>f(0)}\end{array}\right.$,或$\left\{\begin{array}{l}{lo{g}_{2}x<0}\\{f(x)<f(0)}\end{array}\right.$,这样根据f(x)在R上单调递增及y=log2x的单调性便可解出前面的不等式组,从而得出原不等式的解集.
解答 解:f(x)为定义在R上的奇函数;
∴f(0)=0;
∴由log2x•f(x)>0得,$\left\{\begin{array}{l}{lo{g}_{2}x>0}\\{f(x)>f(0)}\end{array}\right.$,或$\left\{\begin{array}{l}{lo{g}_{2}x<0}\\{f(x)<f(0)}\end{array}\right.$;
f(x)在R上单调递增;
∴上面不等式组变成$\left\{\begin{array}{l}{x>1}\\{x>0}\end{array}\right.$,或$\left\{\begin{array}{l}{0<x<1}\\{x<0}\end{array}\right.$;
∴解得x>1;
∴原不等式的解集为(1,+∞).
故答案为:(1,+∞).
点评 考查奇函数的定义,奇函数在原点有定义时,原点处的函数值为0,对数函数的单调性,以及根据单调性定义解不等式的方法.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{3}$ | C. | 1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
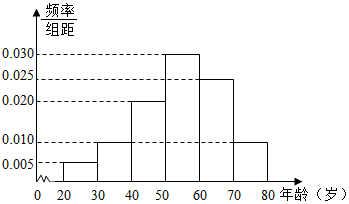 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(cosA) | B. | f(cosA)>f(sinA) | C. | f(cosA)>f(sinB) | D. | f(sinA)>f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com